
分析 由θ是第三象限角,可得$\frac{θ}{2}$为第二或第四象限角,结合|sin$\frac{θ}{2}$|=-sin$\frac{θ}{2}$求得答案.
解答 解:∵θ是第三象限角,∴$π+2kπ<θ<\frac{3π}{2}+2kπ,k∈Z$,
则$\frac{π}{2}+kπ<\frac{θ}{2}<\frac{3π}{4}+kπ,k∈Z$,即$\frac{θ}{2}$为第二或第四象限角,
又|sin$\frac{θ}{2}$|=-sin$\frac{θ}{2}$,
∴$\frac{θ}{2}$为第四象限角.
点评 本题考查三角函数值的符号,考查了象限角的概念,属于基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
| 等级 | 频数 | 频率 |
| 1 | c | a |
| 2 | 4 | b |
| 3 | 9 | 0.45 |
| 4 | 2 | 0.1 |
| 5 | 3 | 0.15 |
| 合计 | 20 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
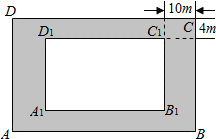 如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m
如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com