
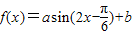
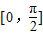 时f(x)的值域为[4,10],求a×b的值;
时f(x)的值域为[4,10],求a×b的值;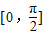 ,知-
,知-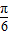
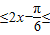
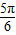 ,由x∈
,由x∈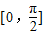 时,函数
时,函数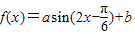 的值域为[4,10],知:当a>0时,
的值域为[4,10],知:当a>0时,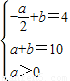 ;当a<0时,
;当a<0时, ,由此能求出a×b.
,由此能求出a×b.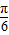 )+b,f(-x)=sin(-2x-
)+b,f(-x)=sin(-2x-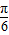 )+b,故函数y=f(-x)的单调增区间满足条件:-
)+b,故函数y=f(-x)的单调增区间满足条件:-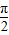 +2kπ≤-2x-
+2kπ≤-2x-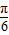 ≤
≤ +2kπ,k∈Z.由此能求出当a=1时,函数y=f(-x)的单调增区间.
+2kπ,k∈Z.由此能求出当a=1时,函数y=f(-x)的单调增区间.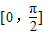 ,∴-
,∴-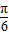
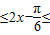
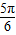 ,
,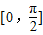 时,函数
时,函数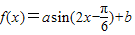 的值域为[4,10],
的值域为[4,10],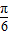 =-
=-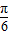 时,f(x)min=asin(-
时,f(x)min=asin(-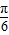 )+b=-
)+b=-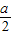 +b=4,
+b=4,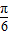 =
=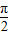 时,f(x)max=asin
时,f(x)max=asin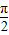 +b=a+b=10,
+b=a+b=10,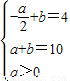 ,得a=4,b=6,
,得a=4,b=6,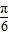 =-
=-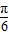 时,f(x)max=asin(-
时,f(x)max=asin(-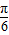 )+b=-
)+b=-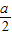 +b=10,
+b=10,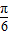 =
=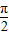 时,f(x)min=asin
时,f(x)min=asin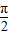 +b=a+b=4,
+b=a+b=4,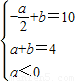 ,得a=-4,b=8,
,得a=-4,b=8,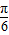 )+b,
)+b, )+b,
)+b,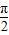 +2kπ≤-2x-
+2kπ≤-2x-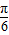 ≤
≤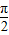 +2kπ,k∈Z.
+2kπ,k∈Z.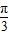 -kπ≤x≤
-kπ≤x≤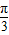 -kπ,k∈Z.
-kπ,k∈Z. -kπ,
-kπ,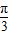 -kπ],k∈Z.
-kπ],k∈Z.

科目:高中数学 来源:2013-2014学年湖南省名校高三上学期第一次大联考理科数学试卷(解析版) 题型:解答题
已知函数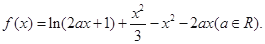
(1)若x=2为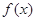 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若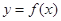 在
在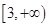 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市九校高三(上)联考数学试卷(文科)(解析版) 题型:解答题
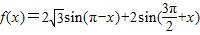
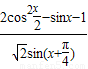 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年黑龙江省哈尔滨三中高二(下)第二次段考数学试卷(文科)(解析版) 题型:解答题
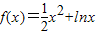
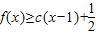 ,求c的取值范围.
,求c的取值范围.查看答案和解析>>
科目:高中数学 来源:2011年湖北省荆州市松滋二中高考数学限时训练(解析版) 题型:解答题
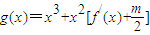 在区间(t,3)上有最值,求实数m取值范围;
在区间(t,3)上有最值,求实数m取值范围;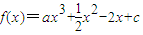
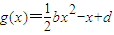 ,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.
,在(1)的条件下,是否存在实数b,使得函数g(x)的图象与函数f(x)的图象恒有含x=-1的三个不同交点?若存在,求出实数b的取值范围;否则说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com