
【题目】已知函数 ![]()
![]() 在
在 ![]() 上单调递增,
上单调递增,
(1)若函数 ![]() 有实数零点,求满足条件的实数
有实数零点,求满足条件的实数 ![]() 的集合
的集合 ![]() ;
;
(2)若对于任意的 ![]() 时,不等式
时,不等式 ![]() 恒成立,求
恒成立,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:函数 ![]() 级
级 ![]() 单调递增区间是
单调递增区间是 ![]() ,因为
,因为 ![]() 在
在 ![]() 上单调递增,所以
上单调递增,所以 ![]() ;
;
令 ![]()
![]() ,则
,则 ![]()
![]()
函数 ![]() 有实数零点,即:
有实数零点,即: ![]() 在
在 ![]() 上有零点,只需:
上有零点,只需:
方法一 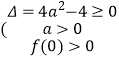 解得
解得 ![]()
方法二 ![]() 解得
解得 ![]()
综上: ![]() ,即
,即 ![]()
(2)解: ![]() 化简得
化简得 ![]()
因为对于任意的 ![]() 时,不等式
时,不等式 ![]() 恒成立,
恒成立,
即对于 ![]() 不等式
不等式 ![]() 恒成立,
恒成立,
设 ![]() (
( ![]() )
)
法一
当 ![]() 时,即
时,即 ![]() 不符合题意
不符合题意
当 ![]() 时,即
时,即 ![]() ,只需
,只需 ![]()
得 ![]() 从而
从而 ![]()
当 ![]() ,即
,即 ![]() ,只需
,只需 ![]()
得 ![]() 或
或 ![]() ,与
,与 ![]() 矛盾
矛盾
法二 ![]() 得
得 ![]()
综上知满足条件的 ![]() 的范围为
的范围为 ![]()
【解析】(1)首先根据二次函数对称轴的位置关系结合函数的增减性得到a的取值范围利用整体思想令 2x = t ( t > 0 )把原函数转化为f ( t ) = t 2 2 a t + 1 t > 0在 ( 0 , + ∞ ) 上有零点即在 ( 0 , + ∞ ) 上有根,结合二次函数图像的性质限制Δ≥0,a>0,f(0)>0得到关于a的不等式组解出即可。(2)结合(1)的结果整理化简不等式转化为当 1 ≤ a ≤ 2 不等式 ( 2x+1 1 ) a + 2 2x 2 > 0 恒成立,由整体思想构造函数 g(x) 关于2x 的二次函数当 1 ≤ a ≤ 2恒成立的问题,结合二次函数在指定区间上的最值问题解出x的取值范围即可。
【考点精析】认真审题,首先需要了解复合函数单调性的判断方法(复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”),还要掌握二次函数在闭区间上的最值(当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】盒中有标号分别为0,1,2,3的球各一个,这些球除标号外均相同.从盒中依次摸取两个球(每次一球,摸出后不放回),记为一次游戏.规定:摸出的两个球上的标号之和等于5为一等奖,等于4为二等奖,等于其它为三等奖.
(1)求完成一次游戏获三等奖的概率;
(2)记完成一次游戏获奖的等级为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?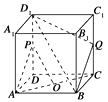
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在直角梯形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .将
.将 ![]() 沿
沿 ![]() 折起,使得点
折起,使得点 ![]() 在平面
在平面 ![]() 的正投影
的正投影 ![]() 恰好落在
恰好落在 ![]() 边上,得到几何体
边上,得到几何体 ![]() ,如图2所示.
,如图2所示.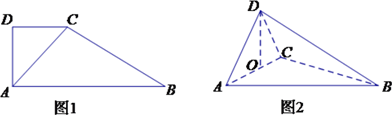
(1)求证: ![]() ;
;
(2)求点 ![]() 到平面
到平面 ![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知c>0,且c≠1,设p:函数y=cx在R上单调递减;q:函数f(x)=x2﹣2cx+1在( ![]() ,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.
,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com