Question

6．已知a，b是空间两条异面直线，它们所成的角为80°，过空间一点P作直线l，使l与a，b所成角均为50°，这样的l有（　　）

• A． 1条
• B． 2条
• C． 3条
• D． 4条

Answer 1

分析 在空间取一点P，经过点P分别作a∥a'，b∥b'，设直线a'、b'确定平面α．由异面直线所成角的定义，得a'、b'所成锐角等于80°，经过P的直线PM的射影P在a'、b'所成锐角的平分线上时，存在两条直线与a'，b'所成的角都是50°，当PM的射影PQ在a'、b'所成钝角的平分线上时，存在1条直线与a'，b'所成的角都是50°，由此可得本题答案．

解答 解：在空间取一点P，经过点P分别作a∥a'，b∥b'，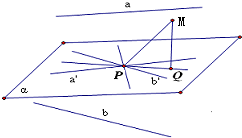
设直线a'、b'确定平面α，
当直线PM满足它的射影PQ在a'、b'所成角的平分线上时，
PM与a'所成的角等于PM与b'所成的角
因为直线a，b所成的角为80°，得a'、b'所成锐角等于80°
所以当PM的射影PQ在a'、b'所成锐角的平分线上时，
PM与a'、b'所成角的范围是[40°，90°）．
这种情况下，过点P有两条直线与a'，b'所成的角都是50°
当PM的射影PQ在a'、b'所成钝角的平分线上时，PM与a'、b'所成角的范围是[50°，90°）．
这种情况下，过点P有且只有一条直线（即PM?α时）与a'，b'所成的角都是50°
综上所述，过空间任意一点P可作与a，b所成的角都是50°的直线有3条
故选：C．

点评 本题给出两条直线所成角为80°，求过空间一点P可作与a，b所成的角都是50°的直线的条数．着重考查了空间两条异面直线所成角及其求法等知识，属于中档题．