
 ,
,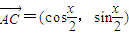 ,其中
,其中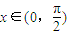 .
.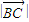 和△ABC的边BC上的高h;
和△ABC的边BC上的高h;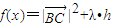 的最大值是5,求常数λ的值.
的最大值是5,求常数λ的值.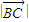 ,
,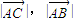 ,结合图象求出BC边上的高;
,结合图象求出BC边上的高;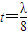 即λ=4时,函数f(x)的最大值为5.
即λ=4时,函数f(x)的最大值为5.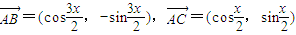 ,∴|
,∴|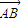 |=|
|=|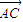 |=1
|=1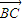 |=
|=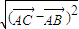 =
=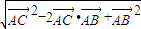 =
=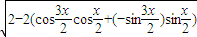
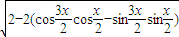 =
=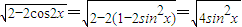 =2|sinx|
=2|sinx|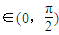 ,∴sinx∈(0,1),∴|
,∴sinx∈(0,1),∴|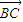 |=2sinx.
|=2sinx. ,△ABC是等腰三角形,
,△ABC是等腰三角形,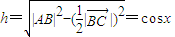
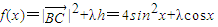 =4(1-cos2x)+λcosx=-4cos2x+λcosx+4
=4(1-cos2x)+λcosx=-4cos2x+λcosx+4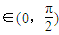 ,∴t∈(0,1)
,∴t∈(0,1)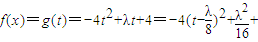 4
4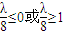 ,即λ≤0或λ≥8时,函数g(t)无最值.
,即λ≤0或λ≥8时,函数g(t)无最值.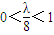 ,即0<λ<8时,f(x)max=
,即0<λ<8时,f(x)max=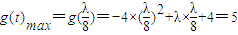


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
| 2S | a+b+c |
查看答案和解析>>
科目:高中数学 来源: 题型:

(2)如图,A![]() 面BCD ,E 、F 、G 、H分别是AB 、BC 、CD 、DA上的点,若EH∩FG=P.求证:P点在直线BD上.
面BCD ,E 、F 、G 、H分别是AB 、BC 、CD 、DA上的点,若EH∩FG=P.求证:P点在直线BD上.

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)△ABC的形状是___________________;
(2)![]() =______________.
=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com