
 ,函数
,函数 的定义域为
的定义域为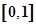 且
且 ,
, 当
当 时有
时有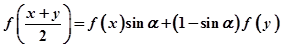
 ;
; 的值;
的值; 的单调增区间.
的单调增区间.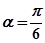
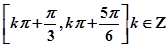 ……12分
……12分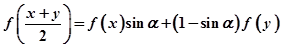 ,根据解题需要给x,y赋予不同的值求解即可.
,根据解题需要给x,y赋予不同的值求解即可.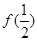 和
和 的值, 令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;根据
的值, 令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;根据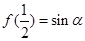 ,所以sinα=3sin²α-2 sin³α从而解出sinα=1/2,求出
,所以sinα=3sin²α-2 sin³α从而解出sinα=1/2,求出 的值.
的值.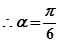 ……8分
……8分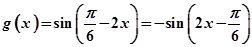
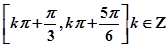 ……12分
……12分

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
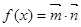 ,其中
,其中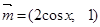 ,
,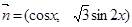
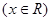 .
.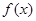 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;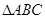 中,
中,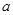 、
、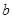 、
、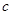 分别是角
分别是角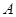 、
、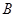 、
、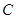 的对边,若
的对边,若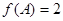 ,
,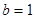 ,
,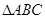 面积为
面积为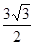 ,求:边
,求:边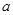 的长及
的长及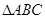 的外接圆半径
的外接圆半径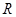 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,函数
,函数 的最大值为
的最大值为 .
. ;
; 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求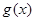 在
在 上的值域.
上的值域.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com