
已知二次函数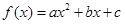 和“伪二次函数”
和“伪二次函数” 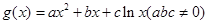 .
.
(Ⅰ)证明:只要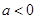 ,无论
,无论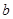 取何值,函数
取何值,函数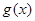 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(Ⅱ)在同一函数图像上任意取不同两点A(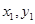 ),B(
),B(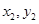 ),线段AB中点为C(
),线段AB中点为C(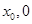 ),记直线AB的斜率为k.
),记直线AB的斜率为k.
(1)对于二次函数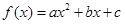 ,求证
,求证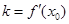 ;
;
(2)对于“伪二次函数” 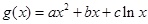 ,是否有(1)同样的性质?证明你的结论。
,是否有(1)同样的性质?证明你的结论。
(Ⅰ)恒成立,当 时,
时, (Ⅱ)恒成立,∵
(Ⅱ)恒成立,∵ ,由二次函数的性质,(Ⅱ)不可能恒成立,则函数
,由二次函数的性质,(Ⅱ)不可能恒成立,则函数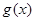 不可能总为增函数.
不可能总为增函数.
(Ⅱ) ;
;
(2)“伪二次函数”  不具有(1)的性质.
不具有(1)的性质.
【解析】
试题分析:(Ⅰ)定义域为 ,如果
,如果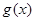 为增函数,则
为增函数,则 (Ⅰ)恒成立,当
(Ⅰ)恒成立,当 时,
时, (Ⅱ)恒成立,∵
(Ⅱ)恒成立,∵ ,由二次函数的性质,(Ⅱ)不可能恒成立,则函数
,由二次函数的性质,(Ⅱ)不可能恒成立,则函数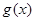 不可能总为增函数.
4分
不可能总为增函数.
4分
(Ⅱ)(1) .
.
由 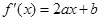 ∴
∴ ,则
,则 8分
8分
(2)不妨设 ,对于“伪二次函数”:
,对于“伪二次函数”:
 (Ⅲ)
(Ⅲ)
由(1)中(Ⅰ)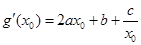 (Ⅳ)
(Ⅳ)
的性质,则 ,比较(Ⅲ)(Ⅳ)两式得
,比较(Ⅲ)(Ⅳ)两式得 ,
,

即 (Ⅴ) 令
(Ⅴ) 令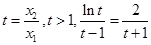 (Ⅵ)
(Ⅵ)
设 ,则
,则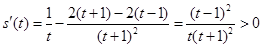
∴ 在(1,
在(1,  )上递增, ∴
)上递增, ∴
∴(Ⅵ)式不可能成立, (Ⅴ)式不可能成立, 
∴“伪二次函数”  不具有(1)的性质.
13分
不具有(1)的性质.
13分
考点:本题主要考查应用导数研究函数的单调性、最值及不等式恒成立问题,不等式的解法。
点评:难题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。(I)中要对a的不同取值情况加以讨论,在解不等式取舍过程中易于出错。涉及不等式恒成立问题,转化成了研究函数的最值,通过构建a的不等式组,求得a的范围。理解“伪函数的概念”的解题的关键之一。


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:2010-2011学年辽宁省高三第四次模拟考试理科数学 题型:解答题
(.(本题满分12分)
已知二次函数 和“伪二次函数”
和“伪二次函数”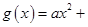
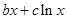 (
(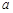 、
、 、
、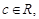
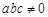 ),
),
(I)证明:只要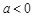 ,无论
,无论 取何值,函数
取何值,函数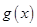 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数 图象上任意取不同两点
图象上任意取不同两点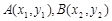 ,线段
,线段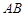 中点的横坐标为
中点的横坐标为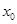 ,记直线
,记直线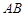 的斜率为
的斜率为 ,
,
(i)求证: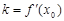 ;
;
(ii)对于“伪二次函数”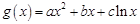 ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高考模拟试题(1) 题型:解答题
已知二次函数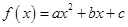 和“伪二次函数”
和“伪二次函数”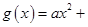
 (
( 、
、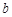 、
、
 ),
),
(I)证明:只要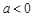 ,无论
,无论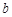 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数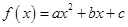 图象上任意取不同两点
图象上任意取不同两点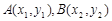 ,线段
,线段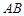 中点的横坐标为
中点的横坐标为 ,记直线
,记直线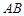 的斜率为
的斜率为 ,
,
(i)求证: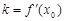 ;
;
(ii)对于“伪二次函数”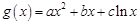 ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
已知二次函数![]() 和“伪二次函数”
和“伪二次函数”![]()
![]() (
(![]() 、
、![]() 、
、![]()
![]() ),
),
(I)证明:只要![]() ,无论
,无论![]() 取何值,函数
取何值,函数![]() 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数![]() 图象上任意取不同两点
图象上任意取不同两点![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,
,
(i)求证:![]() ;
;
(ii)对于“伪二次函数”![]() ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)
已知二次函数![]() 和“伪二次函数”
和“伪二次函数”![]()
![]() (
(![]() 、
、![]() 、
、![]()
![]() ),
),
(I)证明:只要![]() ,无论
,无论![]() 取何值,函数
取何值,函数![]() 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数![]() 图象上任意取不同两点
图象上任意取不同两点![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,
,
(i)求证:![]() ;
;
(ii)对于“伪二次函数”![]() ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com