在△ABC中,若sinA:sinB:sinC=5:7:8,则此三角形的最大角与最小角之和为( )
A.90°
B.120°
C.135°
D.150°
【答案】
分析:设△ABC中三边长 a=5k,b=7k,c=8k,则C为最大角,A为最小角,利用余弦定理求得cosA 和cosC
的值,利用同角三角函数的基本关系 求得sinA 和sinC,利用两角和的余弦公式 求得cos(A+C) 的值,可得 A+C.
解答:解:设△ABC中三边长 a=5k,b=7k,c=8k,则C为最大角,A为最小角.
由余弦定理可得 cosA=
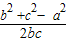
=
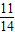
,∴sinA=
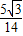
.
cosC=
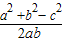
=

,∴sinC=
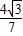
.
故cos(A+C)=cosAcosC-sinsAinC=
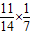
-
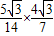
=-

,由于 0<A+C<π,
∴A+C=120°,
故选 B.
点评:本题考查余弦定理,同角三角函数的基本关系,两角和的余弦公式的应用,求出A、C 两个角的正弦和余弦值,是解题的关键.

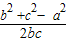 =
=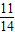 ,∴sinA=
,∴sinA=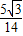 .
.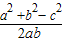 =
= ,∴sinC=
,∴sinC=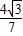 .
.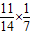 -
-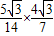 =-
=- ,由于 0<A+C<π,
,由于 0<A+C<π,

 阅读快车系列答案
阅读快车系列答案