
【题目】给定整数![]() ,数列
,数列![]() 、
、![]() 、
、![]() 、
、![]() 每项均为整数,在
每项均为整数,在![]() 中去掉一项
中去掉一项![]() ,并将剩下的数分成个数相同的两组,其中一组数的和与另外一组数的和之差的最大值记为
,并将剩下的数分成个数相同的两组,其中一组数的和与另外一组数的和之差的最大值记为![]() . 将
. 将![]() 、
、![]() 、
、![]() 、
、![]() 中的最小值称为数列
中的最小值称为数列![]() 的特征值.
的特征值.
(Ⅰ)已知数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,写出
,写出![]() 、
、![]() 、
、![]() 的值及
的值及![]() 的特征值;
的特征值;
(Ⅱ)若![]() ,当
,当![]() ,其中
,其中![]() 、
、![]() 且
且![]() 时,判断
时,判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(Ⅲ)已知数列![]() 的特征值为
的特征值为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;
;![]() ;
;![]() .
.![]() 的特征值为
的特征值为![]() ;(Ⅱ)
;(Ⅱ)![]() ,理由见解析;(Ⅲ)最小值为
,理由见解析;(Ⅲ)最小值为![]() .
.
【解析】
(Ⅰ)根据题中的定义可求出![]() 、
、![]() 、
、![]() 的值及
的值及![]() 的特征值;
的特征值;
(Ⅱ)分![]() 、
、![]() 和
和![]() 、
、![]() 两种情况讨论,结合题中定义可证明出
两种情况讨论,结合题中定义可证明出![]() ;
;
(Ⅲ)设![]() ,利用(Ⅱ)中的结论
,利用(Ⅱ)中的结论![]() ,结合数列
,结合数列![]() 的特征值为
的特征值为![]() ,可得出
,可得出![]() ,并证明出
,并证明出![]() ,即可求出
,即可求出![]() 的最小值.
的最小值.
(Ⅰ)由题知:![]() ,
,![]() ,
,![]() ,
,
![]() 的特征值为
的特征值为![]() ;
;
(Ⅱ)![]() .
.
理由如下:由于![]() ,可分下列两种情况讨论:
,可分下列两种情况讨论:
当![]() 、
、![]() 时,
时,
根据定义可知:![]()
![]() ,
,
同理可得:![]() .
.
所以![]() ,所以
,所以![]() .
.
当![]() 、
、![]() 时,同理可得:
时,同理可得:
![]()
![]()
![]() ,
,
所以![]() ,所以
,所以![]() .
.
综上有:![]() ;
;
(Ⅲ)不妨设![]() ,
,
![]()
![]() ,
,
显然,![]() ,
,
![]() .
.
当且仅当![]() 时取等号;
时取等号;![]() .
.
当且仅当![]() 时取等号;
时取等号;
由(Ⅱ)可知![]() 、
、![]() 的较小值为
的较小值为![]() ,
,
所以![]() .
.
当且仅当![]() 时取等号,
时取等号,
此时数列![]() 为常数列,其特征值为
为常数列,其特征值为![]() ,不符合题意,则必有
,不符合题意,则必有
![]() .
.
下证:若![]() ,
,![]() ,总有
,总有![]() .
.
证明:![]()
![]() .
.
所以![]() .
.
因此![]()
![]() .
.
当![]() 时,
时,![]() 可取到最小值
可取到最小值![]() ,符合题意.
,符合题意.
所以![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,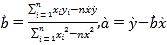 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 与
与![]() 的图象在
的图象在![]() 处有相同的切线,求
处有相同的切线,求![]() 的值;
的值;
(2)当![]() 时,若对任意
时,若对任意![]() 和任意
和任意![]() ,总存在不相等的正实数
,总存在不相等的正实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)当![]() 时,设函数
时,设函数![]() 与
与![]() 的图象交于
的图象交于![]()
![]() 两点.求证:
两点.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}(an∈Z)的前n项和为Sn,记S1,S2,…,Sn中奇数的个数为bn.
(1)若an=n,请写出数列{bn}的前5项;
(2)求证:“a1为奇数,ai(i=2,3,4,…)为偶数”是“数列{bn}是单调递增数列”的充分不必要条件;
(3)若ai=bi,i=1,2,3,…,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com