
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,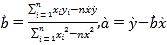 .
.
【答案】(1)![]() ,预计到2022年该公司的网购人数能超过300万人;
,预计到2022年该公司的网购人数能超过300万人;
(2)约400元.
【解析】
(1)依题意,先求出![]() ,代入公式即可得到
,代入公式即可得到![]() ,
,![]() ,可得回归方程为
,可得回归方程为![]() ,令
,令![]() ,
,![]() .所以预计到2022年该公司的网购人数能超过300万;
.所以预计到2022年该公司的网购人数能超过300万;
(2)遥控车移到第![]() (
(![]() )格的情况是下列两种,而且也只有两种.
)格的情况是下列两种,而且也只有两种.
①遥控车先到第![]() 格,又掷出偶数,其概率为
格,又掷出偶数,其概率为![]()
②遥控车先到第![]() 格,又掷出奇数,其概率为
格,又掷出奇数,其概率为![]()
所以![]() ,即可证得
,即可证得![]() 是等比数列,
是等比数列,
利用累加法求出数列![]() 的通项公式,即可求得失败和获胜的概率,从而计算出期望.
的通项公式,即可求得失败和获胜的概率,从而计算出期望.
解:(1)![]()
![]()
![]()
![]()
故![]() 从而
从而![]()
所以所求线性回归方程为![]() ,
,
令![]() ,解得
,解得![]() .
.
故预计到2022年该公司的网购人数能超过300万人
(2)遥控车开始在第0格为必然事件,![]() ,第一次掷骰子出现奇数,遥控车移到第一格,其概率为
,第一次掷骰子出现奇数,遥控车移到第一格,其概率为![]() ,即
,即![]() .遥控车移到第
.遥控车移到第![]() (
(![]() )格的情况是下列两种,而且也只有两种.
)格的情况是下列两种,而且也只有两种.
①遥控车先到第![]() 格,又掷出奇数,其概率为
格,又掷出奇数,其概率为![]()
②遥控车先到第![]() 格,又掷出偶数,其概率为
格,又掷出偶数,其概率为![]()
所以![]() ,
,![]()
![]() 当
当![]() 时,数列
时,数列![]() 是公比为
是公比为![]() 的等比数列
的等比数列
![]()
以上各式相加,得![]()
![]()
![]() (
(![]() ),
),
![]() 获胜的概率
获胜的概率![]()
失败的概率![]()
![]() 设参与游戏一次的顾客获得优惠券金额为
设参与游戏一次的顾客获得优惠券金额为![]() 元,
元,![]() 或
或![]()
![]() X的期望
X的期望![]()
![]() 参与游戏一次的顾客获得优惠券金额的期望值为
参与游戏一次的顾客获得优惠券金额的期望值为![]() ,约400元.
,约400元.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
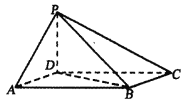
(1)求证:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若![]() ,求点A到平面
,求点A到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次数学考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班样本成绩的茎叶图如图所示.
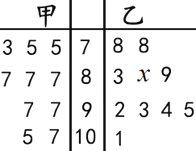
(1)用样本估计总体,若根据茎叶图计算得甲乙两个班级的平均分相同,求![]() 的值;
的值;
(2)从样本中任意抽取3名学生的成绩,若至少有两名学生的成绩相同的概率大于![]() ,则该班成绩判断为可疑.试判断甲班的成绩是否可疑?并说明理由.
,则该班成绩判断为可疑.试判断甲班的成绩是否可疑?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,直线
轴正半轴为极轴,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 交圆
交圆![]() 于
于![]() 两点,
两点,![]() 为
为![]() 中点.
中点.
(1)求点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,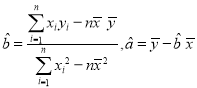 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,梯形![]() 中,
中,![]() ,过
,过![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.![]() ,
,![]() ,已知
,已知![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2.
,如图2.
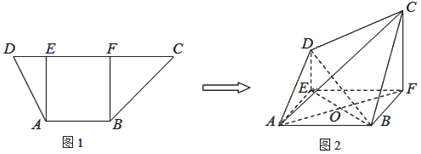
(1)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(2)在(1)的条件下,若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数,若对任何实数
上的函数,若对任何实数![]() 以及
以及![]() 中的任意两数
中的任意两数![]() 、
、![]() ,恒有
,恒有![]() ,则称
,则称![]() 为定义在
为定义在![]() 上的
上的![]() 函数.
函数.
(1)证明函数![]() 是定义域上的
是定义域上的![]() 函数;
函数;
(2)判断函数![]() 是否为定义域上的
是否为定义域上的![]() 函数,请说明理由;
函数,请说明理由;
(3)若![]() 是定义域为
是定义域为![]() 的函数,且最小正周期为
的函数,且最小正周期为![]() ,试证明
,试证明![]() 不是
不是![]() 上的
上的![]() 函数.
函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,记
,记![]()
![]() ;
;
(1)求实数![]() 、
、![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)对于定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() ,用任意的
,用任意的![]()
![]() 将
将![]() 划分为
划分为![]() 个小区间,其中
个小区间,其中![]() ,若存在一个常数
,若存在一个常数![]() ,使得
,使得![]()
![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的有界变差函数;
上的有界变差函数;
①试证明函数![]() 是在
是在![]() 上的有界变差函数,并求出
上的有界变差函数,并求出![]() 的最小值;
的最小值;
②写出![]() 是在
是在![]() 上的有界变差函数的一个充分条件,使上述结论成为其特例;(不要求证明)
上的有界变差函数的一个充分条件,使上述结论成为其特例;(不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定整数![]() ,数列
,数列![]() 、
、![]() 、
、![]() 、
、![]() 每项均为整数,在
每项均为整数,在![]() 中去掉一项
中去掉一项![]() ,并将剩下的数分成个数相同的两组,其中一组数的和与另外一组数的和之差的最大值记为
,并将剩下的数分成个数相同的两组,其中一组数的和与另外一组数的和之差的最大值记为![]() . 将
. 将![]() 、
、![]() 、
、![]() 、
、![]() 中的最小值称为数列
中的最小值称为数列![]() 的特征值.
的特征值.
(Ⅰ)已知数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,写出
,写出![]() 、
、![]() 、
、![]() 的值及
的值及![]() 的特征值;
的特征值;
(Ⅱ)若![]() ,当
,当![]() ,其中
,其中![]() 、
、![]() 且
且![]() 时,判断
时,判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(Ⅲ)已知数列![]() 的特征值为
的特征值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com