
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(Ⅰ)由题意求得a,b的值即可确定椭圆方程;
(Ⅱ)分类讨论,设直线l代入椭圆方程,运用韦达定理和弦长公式,可得|AB|,根据点到直线的距离公式可求出|CD|,再由四边形的面积公式,化简整理,运用不等式的性质,即可得到所求范围
试题解析:
(1)由题意知![]() ,则
,则![]() ,
,
圆![]() 的标准方程为
的标准方程为![]() ,从而椭圆的左焦点为
,从而椭圆的左焦点为![]() ,即
,即![]() ,
,
所以![]() ,又
,又![]() ,得
,得![]() .
.
所以椭圆的方程为:![]() .
.
(2)可知椭圆右焦点![]() .
.
(ⅰ)当l与x轴垂直时,此时![]() 不存在,直线l:
不存在,直线l:![]() ,直线
,直线![]() ,
,
可得:![]() ,
,![]() ,四边形
,四边形![]() 面积为12.
面积为12.
(ⅱ)当l与x轴平行时,此时![]() ,直线
,直线![]() ,直线
,直线![]() ,
,
可得:![]() ,
,![]() ,四边形
,四边形![]() 面积为
面积为![]() .
.
(iii)当l与x轴不垂直时,设l的方程为![]()
![]() ,并设
,并设![]() ,
,![]() .
.
由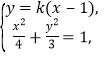 得
得![]() .
.
显然![]() ,且
,且![]() ,
, ![]() .
.
所以![]() .
.
过![]() 且与l垂直的直线
且与l垂直的直线![]() ,则圆心到
,则圆心到![]() 的距离为
的距离为![]() ,
,
所以![]() .
.
故四边形![]() 面积:
面积:![]() .
.
可得当l与x轴不垂直时,四边形![]() 面积的取值范围为(12,
面积的取值范围为(12,![]() ).
).
综上,四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆于
轴的垂线交椭圆于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为椭圆
为椭圆![]() 短轴的上顶点,直线
短轴的上顶点,直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率的和为
的斜率的和为![]() ,问:直线
,问:直线![]() 是否过定点?若是,求出这个定点,否则说明理由.
是否过定点?若是,求出这个定点,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中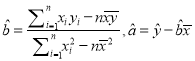
(注: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过函数性质的学习,我们知道:“函数![]() 的图象关于
的图象关于![]() 轴成轴对称图形”的充要条件是“
轴成轴对称图形”的充要条件是“![]() 为偶函数”.
为偶函数”.
(1)若![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并求不等式
的解析式,并求不等式![]() 的解集;
的解集;
(2)某数学学习小组针对上述结论进行探究,得到一个真命题:“函数![]() 的图象关于直线
的图象关于直线![]() 成轴对称图形”的充要条件是“
成轴对称图形”的充要条件是“![]() 为偶函数”.若函数
为偶函数”.若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() .
.
(i)求![]() 的解析式;
的解析式;
(ii)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】右图是一个几何体的平面展开图,其中ABCD为
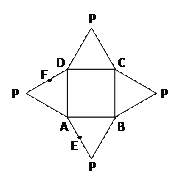
正方形, E、F分别为PA、PD的中点,在此几何体中,
给出下面四个结论:
①直线BE与直线CF异面;②直线BE与直线AF异面;
③直线EF//平面PBC; ④平面BCE⊥平面PAD.
其中正确结论的个数是
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2名男生和2名女生中任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com