
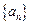 满足
满足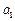 =0,
=0,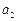 =2,
=2,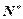 都有
都有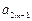 +
+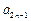 =
=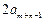 +
+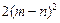
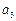 ,
,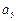 ;
;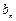 =
=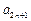 -
-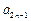 ( n∈
( n∈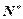 ),证明:
),证明: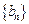 是等差数列;
是等差数列;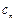 =(
=(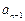 -
-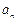 )
)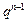 ( q≠0,n∈
( q≠0,n∈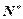 ),求数列的前n项的和
),求数列的前n项的和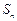 .
.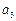 =
= -
-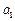 +2=6,再令m=3,n=1,可得
+2=6,再令m=3,n=1,可得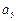 =
=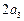 -
-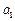 +8=20.
+8=20.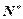 时,由已知(以n+2代替m)可得
时,由已知(以n+2代替m)可得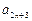 +
+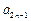 =
=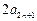 +8,于是[
+8,于是[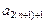 -
-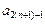 ]-(
]-(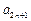 -
-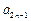 )=8,即
)=8,即 -
-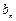 =8.所以
=8.所以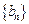 是公差为8的等差数列.
是公差为8的等差数列.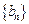 是首项
是首项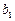 =
=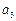 -
-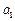 =6,公差为8的等差数列,则
=6,公差为8的等差数列,则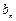 =8n-2,即
=8n-2,即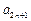 -
-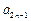 =8n-2.另由已知(令m=1)可得,
=8n-2.另由已知(令m=1)可得,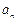 =
=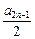 -
-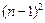 .那么
.那么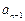 -
-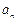 =
=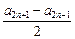 -2n+1=
-2n+1=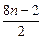 -2n+1=2n,于是
-2n+1=2n,于是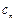 =
=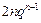 .
.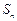 =2+4+6+…+2n=n (n+1).
=2+4+6+…+2n=n (n+1).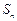 =2·
=2·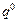 +4·
+4·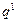 +6·
+6·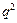 +…+2n·
+…+2n·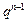 ,两边同乘以q,可得
,两边同乘以q,可得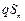 =2·
=2·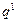 +4·
+4·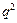 +6·
+6·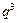 +…+2n·
+…+2n·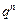 .上述两式相减,得
.上述两式相减,得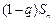 =
=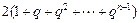 -2n
-2n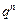 =
=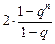 -2n
-2n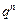 =
= ,
,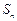 =
=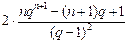 .
.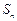 =
=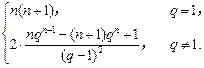


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com