
设直线l:x-y+m=0与抛物线C:y2=4x交于不同两点A,B,F 为抛物线的焦点.
(1)求△ABF的重心G的轨迹方程;
(2)如果m=-2,求△ABF的外接圆的方程.
(1)y=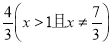 (2)
(2)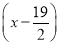 2+
2+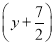 2=
2=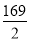
【解析】(1)设A(x1,y1),B(x2,y2),F(1,0),重心G(x,y),
 ⇒y2-4y+4m=0,
⇒y2-4y+4m=0,
∴Δ>0⇒m<1且m≠-1(A,B,F不共线),
故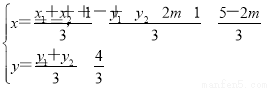
∴重心G的轨迹方程为y=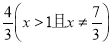 .
.
(2)若m=-2,则y2-4y-8=0,设AB中点为(x0,y0,)
∴y0=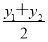 =2,∴x0=y0-m=2-m=4,
=2,∴x0=y0-m=2-m=4,
那么AB的中垂线方程为x+y-6=0,
令△ABF的外接圆圆心为C(a,6-a),
又|AB|=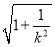 |y1-y2|=4
|y1-y2|=4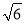 ,C到AB的距离为d=
,C到AB的距离为d=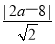 ,∴|CA|=|CF|⇒(2
,∴|CA|=|CF|⇒(2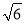 )2+
)2+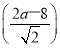 2=(a-1)2+(6-a)2⇒a=
2=(a-1)2+(6-a)2⇒a=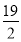 ,
,
∴C点的坐标为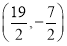 ,∴|CF|2=
,∴|CF|2=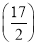 2+
2+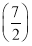 2=
2=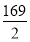 ,
,
∴所求的圆的方程为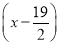 2+
2+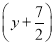 2=
2=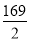 .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
若双曲线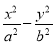 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=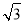 x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).
A.(1,2) B.(1,2] C.(1,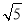 ) D.(1,
) D.(1,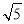 ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知两条不同的直线m,n和两个不同的平面α,β,给出下列四个命题:
①若m∥α,n∥β,且α∥β,则m∥n;②若m∥α,n⊥β,且α⊥β,则m∥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m⊥α,n⊥β,且α⊥β,则m⊥n.其中正确的个数有( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
正项数列{an}的前n项和Sn满足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn= ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:选择题
在等差数列{an}中,a1=142,d=-2,从第一项起,每隔两项取出一项,构成新的数列{bn},则此数列的前n项和Sn取得最大值时n的值是( ).
A.23 B.24 C.25 D.26
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:填空题
已知双曲线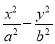 =1(a>0,b>0)的渐近线方程为y=±
=1(a>0,b>0)的渐近线方程为y=±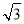 x,则它的离心率为________.
x,则它的离心率为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( ).
A.内切 B.相交
C.外切 D.相离
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
已知随机变量X~N(1,4)且P(X<2)=0.72,则P(1<X<2)等于( ).
A.0.36 B.0.16 C.0.22 D.0.28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com