
【题目】如图①,利用斜二侧画法得到水平放置的![]() 的直观图
的直观图![]() ,其中
,其中![]() 轴,
轴,![]() 轴.若
轴.若![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,记
,记![]() ,执行如图②的框图,则输出
,执行如图②的框图,则输出![]() 的值
的值
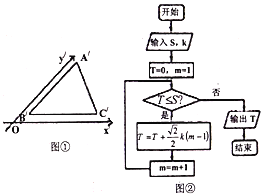
A. 12B. 10C. 9D. 6
【答案】A
【解析】
由斜二侧画法的画图法则,结合已知可求出S及k值,模拟程序的运行过程,分析变量T的值与S值的关系,可得答案.
∵在直观图△A′B′C′中,A′B′=B′C′=3,
∴S′![]() A′B′B′C′sin45°
A′B′B′C′sin45°![]()
由斜二侧画法的画图法则,可得在△ABC中,AB=6.BC=3,且AB⊥BC
∴S![]() ABBC=9
ABBC=9
则由S=kS′得k=2![]() ,则T=T
,则T=T![]() (m﹣1)=T
(m﹣1)=T![]() 2(m﹣1)
2(m﹣1)
故执行循环前,S=9,k=2![]() ,T=0,m=1,满足进行循环的条件,执行循环体后,T=0,m=2
,T=0,m=1,满足进行循环的条件,执行循环体后,T=0,m=2
当T=0,m=2时,满足进行循环的条件,执行循环体后,T=2,m=3
当T=2,m=3时,满足进行循环的条件,执行循环体后,T=6,m=4
当T=6,m=4时,满足进行循环的条件,执行循环体后,T=12,m=5
当T=12,m=5时,不满足进行循环的条件,退出循环后,T=12,
故输出的结果为12
故选:A.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取![]() 名学生,将他们的期中考试数学成绩(满分
名学生,将他们的期中考试数学成绩(满分![]() 分,成绩均为不低于
分,成绩均为不低于![]() 分的整数)分成六段:
分的整数)分成六段:![]() ,
,![]() ,…,
,…,![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
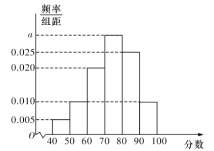
(1)求图中实数![]() 的值;
的值;
(2)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对以下命题:
①随机事件的概率与频率一样,与试验重复的次数有关;
②抛掷两枚均匀硬币一次,出现一正一反的概率是![]() ;
;
③若一种彩票买一张中奖的概率是![]() ,则买这种彩票一千张就会中奖;
,则买这种彩票一千张就会中奖;
④“姚明投篮一次,求投中的概率”属于古典概型概率问题.
其中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点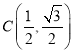 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心,半径为
为圆心,半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应低碳绿色出行,某市推出“新能源分时租赁汽车”,其中一款新能源分时租赁汽车,每次租车收费得标准由以下两部分组成:(1)根据行驶里程数按1元/公里计费;(2)当租车时间不超过40分钟时,按0.12元/分钟计费;当租车时间超过40分钟时,超出的部分按0.20元/分钟计费;(3)租车时间不足1分钟,按1分钟计算.已知张先生从家里到公司的距离为15公里,每天租用该款汽车上下班各一次,且每次租车时间t20,60(单位:分钟).由于堵车,红绿灯等因素,每次路上租车时间t是一个随即变量.现统计了他50次路上租车时间,整理后得到下表:
租车时间t(分钟) | [20,30] | (30,40] | (40,50] | (50,60] |
频数 | 2 | 18 | 20 | 10 |
将上述租车时间的频率视为概率.
(1)写出张先生一次租车费用y(元)与租车时间t(分钟)的函数关系式;
(2)公司规定,员工上下班可以免费乘坐公司接送车,若不乘坐公司接送车的每月(按22天计算)给800元车补.从经济收入的角度分析,张先生上下班应该选择公司接送车,还是租用该款新能源汽车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如城镇小汽车的普及率为75%,即平均每100个家庭有75个家庭拥有小汽车,若从如城镇中任意选出5个家庭,则下列结论成立的是( )
A.这5个家庭均有小汽车的概率为![]()
B.这5个家庭中,恰有三个家庭拥有小汽车的概率为![]()
C.这5个家庭平均有3.75个家庭拥有小汽车
D.这5个家庭中,四个家庭以上(含四个家庭)拥有小汽车的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
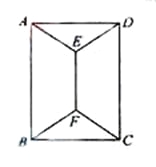
A.288种B.264种C.240种D.168种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com