
已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P,Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径.
解 法一 将x=3-2y,
代入方程x2+y2+x-6y+m=0,
得5y2-20y+12+m=0.
设P(x1,y1),Q(x2,y2),
则y1,y2满足条件:
y1+y2=4,y1y2=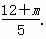 .
.
∵OP⊥OQ,∴x1x2+y1y2=0.
而x1=3-2y1,x2=3-2y2.
∵x1x2=9-6(y1+y2)+4y1y2=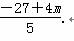 .
.
故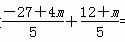 =0,解得m=3,
=0,解得m=3,
此时Δ=(-20)2-4×5×(12+m)=20(8-m)>0,圆心坐标为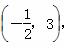 ,半径r=
,半径r=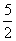 .
.
法二 如图所示,设弦PQ中点为M,且圆x2+y2+x-6y+m=0的圆心为O1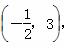 ,
,
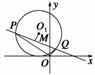 设M(x0,y0),P(x1,y1),Q(x2,y2),
设M(x0,y0),P(x1,y1),Q(x2,y2),
由法一知,y1+y2=4,x1+x2=-2,
∴x0=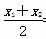 =-1,y0=
=-1,y0=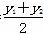 =2.
=2.
即M的坐标为(-1,2).
则以PQ为直径的圆可设为(x+1)2+
(y-2)2=r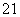 .
.
∵OP⊥OQ,∴点O在以PQ为直径的圆上.
∴(0+1)2+(0-2)2=r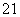 ,即r
,即r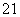 =5,|MQ|2=r
=5,|MQ|2=r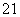 .
.
在Rt△O1MQ中,|O1Q|2=|O1M|2+|MQ|2.
∴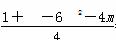 =
=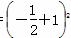 +(3-2)2+5.
+(3-2)2+5.
∴m=3,∴圆心坐标为 ,半径r=
,半径r=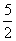 .
.


科目:高中数学 来源: 题型:
设两条直线的方程分别为x+y+a=0和x+y+b=0,已知a,b是关于x的方程x2+x+c=0的两个实数根,且0≤c≤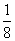 ,则这两条直线之间的距离的最大值和最小值分别为( ).
,则这两条直线之间的距离的最大值和最小值分别为( ).
A.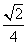 ,
,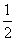 B.
B.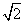 ,
,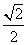 C.
C.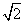 ,
,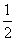 D.
D.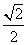 ,
,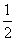
查看答案和解析>>
科目:高中数学 来源: 题型:
若圆x2+y2-2ax+3by=0的圆心位于第三象限,那么直线x+ay+b=0一定不经过( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源: 题型:
求适合下列条件的圆的方程:
(1)圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2);
(2)过三点A(1,12),B(7,10),C(-9,2).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)求m=45时两圆的公共弦所在直线的方程和公共弦的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.
(1)求椭圆离心率的范围;
(2)求证:△F1PF2的面积只与椭圆的短轴长有关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com