
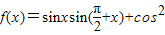 x,在△ABC中,角A、B、C的对边分别为a,b,c
x,在△ABC中,角A、B、C的对边分别为a,b,c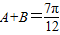 ,
,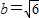 ,求A和a.
,求A和a.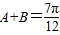 ,求出B的值,结合
,求出B的值,结合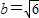 ,利用正弦定理求出a,即可.
,利用正弦定理求出a,即可.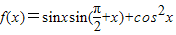 =sinxcosx+cos2x…(1分)
=sinxcosx+cos2x…(1分)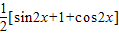 …(3分)
…(3分)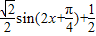 .…(4分)
.…(4分)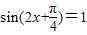 ,
,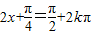 ,
,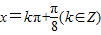 时,f(x)取得最大值,…(5分)
时,f(x)取得最大值,…(5分)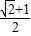 .…(6分)
.…(6分)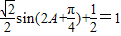 ,
,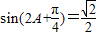 .…(7分)
.…(7分)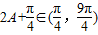 .
.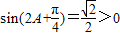 ,
, ,
,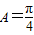 .…(9分)
.…(9分)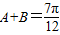 ,所以
,所以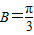 .…(10分)
.…(10分)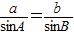 及
及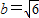 ,
,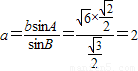 .…(12分)
.…(12分)

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年广东省山一高二上学期第二次月考理科数学卷 题型:选择题
“若f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2……xn,有
[f(x1)+f(x2)+……+f(xn)]≤f()。”设f(x)=sinx在(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值是( )
A.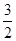 B.
B.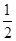
 C.
C.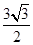 D.
D.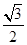
查看答案和解析>>
科目:高中数学 来源:0119 月考题 题型:单选题
 )。”设f(x)=sinx在(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值是
)。”设f(x)=sinx在(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值是



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com