Question

14．函数f（x）=（x-$\frac{1}{x}$）sinx（-π≤x＜0或0＜x≤π）的图象大致为（　　）

• A．
• B．
• C．
• D．

Answer 1

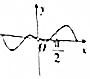分析 判断f（x）的奇偶性，零点个数，计算f（$\frac{π}{2}$），即可得出答案．

解答 解：∵f（-x）=（-x+$\frac{1}{x}$）sin（-x）=（x-$\frac{1}{x}$）sinx=f（x），
∴f（x）是偶函数，即f（x）的图象关于y轴对称，
排除D，
令f（x）=0得x-$\frac{1}{x}$=0或sinx=0，
∵-π≤x＜0或0＜x≤π，
∴x=1或x=-1或x=-π或x=π．
∴f（x）有4个零点，排除A，
又f（$\frac{π}{2}$）=$\frac{π}{2}$-$\frac{2}{π}$＞0，排除C，
故选B．

点评 本题考查了函数图象的判断，主要从奇偶性、单调性、零点、函数值等各方面判断，属于中档题．