
如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.

(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.
(1)由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形,且∠ACB=90°.
连结A1C,设A1C∩AC1=O,连结MO,
由题意可知,得到MO∥B1C,进一步得到B1C∥平面AC1M.
(2)利用已知得到C1M⊥A1B1,
根据平面A1B1C1⊥平面AA1B1B,
得到C1M⊥平面AA1B1B,达到证明目的:平面AC1M⊥平面AA1B1B.
【解析】
试题分析:
思路分析:首先,由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形。(1)小题,为证明B1C∥平面AC1M,只需证明B1C平行于平面AC1M内的任一直线,发现、构造这样的一条直线是关键。通过连结A1C,并设A1C∩AC1=O,则MO即为这样的直线。
(2)小题,为证明“面面垂直”,须注明“线面垂直”。由等腰三角形底边的中线,发现垂直关系。
证明:(1)由三视图可知三棱柱A1B1C1—ABC为直三棱柱,底面是等腰直角三角形,且∠ACB=90°.
连结A1C,设A1C∩AC1=O,连结MO,
由题意可知,A1O=CO,A1M=B1M,
∴MO∥B1C,
又MO⊂平面AC1M,
B1C⊄平面AC1M,∴B1C∥平面AC1M.
(2)∵A1C1=B1C1,M为A1B1的中点,
∴C1M⊥A1B1,
又平面A1B1C1⊥平面AA1B1B,
平面A1B1C1∩平面AA1B1B=A1B1,
∴C1M⊥平面AA1B1B,又 ,所以,平面AC1M⊥平面AA1B1B.
,所以,平面AC1M⊥平面AA1B1B.
考点:三视图,三棱柱的几何特征,平行关系,垂直关系。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。三视图问题,关键是理解三视图的画法规则,应用“长对正,高平齐,宽相等”,确定数据。认识几何体的几何特征,是解题的关键之一。


科目:高中数学 来源: 题型:
 (2012•淮北一模)如图所示,三棱柱ABC-A1B1Cl中,AB=AC=AA1=2,面ABC1⊥面AAlClC,∠AAlCl=∠BAC1=600,
(2012•淮北一模)如图所示,三棱柱ABC-A1B1Cl中,AB=AC=AA1=2,面ABC1⊥面AAlClC,∠AAlCl=∠BAC1=600,查看答案和解析>>
科目:高中数学 来源: 题型:
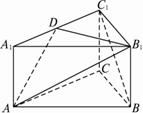
(1)确定点D的位置,并证明你的结论;
(2)求二面角A1 –AB-1D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
 | |||
 | |||
查看答案和解析>>
科目:高中数学 来源:安徽省模拟题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012年安徽省淮北市高考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com