
【题目】下列四个命题中,真命题有 . (写出所有真命题的序号)
①若a,b,c∈R,则“ac2>bc2”是“a>b”成立的充分不必要条件;②命题“x0∈R, ![]() +x0+1<0”的否定是“x∈R,x2+x+1≥0”;③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;④函数f(x)=ln x+x-
+x0+1<0”的否定是“x∈R,x2+x+1≥0”;③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;④函数f(x)=ln x+x- ![]() 在区间(1,2)上有且仅有一个零点.
在区间(1,2)上有且仅有一个零点.
【答案】①②③④
【解析】①若c=0,则不论a,b的大小关系如何,都有ac2=bc2 , 而若ac2>bc2 , 则有a>b,故“ac2>bc2”是“a>b”成立的充分不必要条件,故①为真命题;②特称命题的否定是全称命题,故命题“x0∈R, ![]() +x0+1<0”的否定是“x∈R,x2+x+1≥0”,故②为真命题;③命题“若p,则q”形式的命题的否命题是“若
+x0+1<0”的否定是“x∈R,x2+x+1≥0”,故②为真命题;③命题“若p,则q”形式的命题的否命题是“若 ![]() ,则
,则 ![]() ”,故命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”,故③为真命题;④由于f(1)f(2)=
”,故命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”,故③为真命题;④由于f(1)f(2)= ![]() ,则函数f(x)=ln x+x-
,则函数f(x)=ln x+x- ![]() 在区间(1,2)上存在零点,又函数f(x)=ln x+x-
在区间(1,2)上存在零点,又函数f(x)=ln x+x- ![]() 在区间(1,2)上为增函数,所以函数f(x)=ln x+x-
在区间(1,2)上为增函数,所以函数f(x)=ln x+x- ![]() 在区间(1,2)上有且仅有一个零点,故④为真命题.①由充分必要条件的定义,注意举反例,即可判断;
在区间(1,2)上有且仅有一个零点,故④为真命题.①由充分必要条件的定义,注意举反例,即可判断;
②由含有一个量词的命题的否定形式,即可判断;
③由命题的否命题,既要对条件否定,也要对结论否定,注意否定形式,可判断;
④先通过导数判断函数的单调性,再由零点存在定理,即可判断.该部分内容是《课程标准》新增加的内容,几乎年年都考,涉及知识点多而且全,多以小题形式出现.


科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若sinA=cos( ![]() ﹣B),a=3,c=2.
﹣B),a=3,c=2.
(1)求 ![]() 的值;
的值;
(2)求tan( ![]() ﹣B)的值.
﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在以
为参数),在以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 ![]() 是圆心为
是圆心为 ![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线 ![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设 ![]() 为曲线
为曲线 ![]() 上的点,
上的点, ![]() 为曲线
为曲线 ![]() 上的点,求
上的点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①x∈R,不等式x2+2x>4x-3均成立;
②若log2x+logx2≥2,则x>1;
③“若a>b>0且c<0,则 ![]() ”的逆否命题;
”的逆否命题;
④若p且q为假命题,则p,q均为假命题.
其中真命题是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是偶函数,当x>0时,f(x)单调递减,设a=-21.2 , ![]() ,c=2log52,则f(a),f(b),f(c)的大小关系为( )
,c=2log52,则f(a),f(b),f(c)的大小关系为( )
A.f(c)<f(b)<f(a)
B.f(c)<f(a)<f(b)
C.f(c)>f(b)>f(a)
D.f(c)>f(a)>f(b)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= 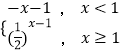 的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
A.a>1
B.a≤﹣ ![]()
C.a≥1或a<﹣ ![]()
D.a>1或a≤﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com