
如图,在四棱锥A-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(1)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(2)求证:平面BDE⊥平面SAC;
(3)当二面角E-BD-C的大小为45°时,试判断点E在SC上的位置,并说明理由.

(Ⅰ)连接 ,由条件可得
,由条件可得 ∥
∥ .
.
因为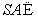 平面
平面 ,
, 平面
平面 ,
,
所以 ∥平面
∥平面 .
.
(Ⅱ)法一:证明:由已知可得,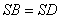 ,
, 是
是 中点,
中点,
所以 ,
,
又因为四边形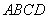 是正方形,所以
是正方形,所以 .
.
因为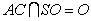 ,所以
,所以 .
.
又因为 ,所以平面
,所以平面 平面
平面 . -
. -
(Ⅱ)法二:证明:由(Ⅰ)知 ,
, .
.
建立如图所示的空间直角坐标系.
设四棱锥 的底面边长为2,
的底面边长为2,
则 ,
, ,
, ,
,
 ,
, ,
, .
.
所以 ,
, .
.
设 (
( ),由已知可求得
),由已知可求得 .
.
所以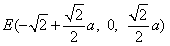 ,
, .
.
设平面 法向量为
法向量为 ,
,
则 即
即
令 ,得
,得 .
.
易知 是平面
是平面 的法向量.
的法向量.
因为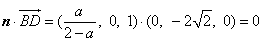 ,
,
所以 ,所以平面
,所以平面 平面
平面 . -------------------(8分)
. -------------------(8分)
(Ⅲ)解:设 (
( ),由(Ⅱ)可知,
),由(Ⅱ)可知,
平面 法向量为
法向量为 .
.
因为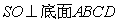 ,
,
所以 是平面
是平面 的一个法向量.
的一个法向量.
由已知二面角 的大小为
的大小为 .
.
所以 ,
,
所以 ,解得
,解得 .
.
所以点 是
是 的中点.
的中点.
【解析】略


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
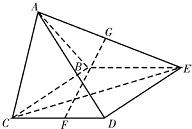 如图,在四棱锥A-BCDE中,底面BCDE为矩形,AB=AC,BC=2,CD=1,并且侧面ABC⊥底面BCDE.
如图,在四棱锥A-BCDE中,底面BCDE为矩形,AB=AC,BC=2,CD=1,并且侧面ABC⊥底面BCDE.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:
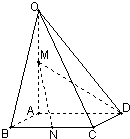 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
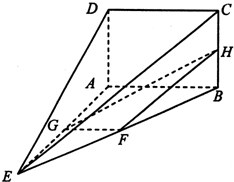 (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点| GP |
| GF |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
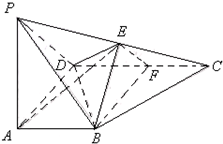 如图,在四棱锥P-ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点,DE=EC.
如图,在四棱锥P-ABCD中,PA⊥AD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点,DE=EC.| π |
| 4 |
| π |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com