
 的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图和直观图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形. 是侧棱
是侧棱 上的动点.
上的动点.

 ;
; 为
为 的中点,求直线
的中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. 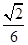 ;(3)
;(3)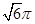
 ,要转到线面垂直,通过观察需证明
,要转到线面垂直,通过观察需证明 平面
平面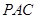 .所以要证明
.所以要证明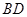 垂直于平面两条相交直线,显然
垂直于平面两条相交直线,显然 ,
,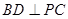 .从而可得结论.
.从而可得结论. 与平面
与平面 所成角的正弦值,需要找到直线与平面所成的角.通过证明平面
所成角的正弦值,需要找到直线与平面所成的角.通过证明平面
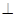 平面
平面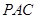 .即可得到点E到平面
.即可得到点E到平面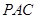 的投影在PO(O是AC与BD的交点)上.这样就可以求出直线与平面所成的角,再通运算即可求出结论.本小题也可已建立空间坐标系来求.
的投影在PO(O是AC与BD的交点)上.这样就可以求出直线与平面所成的角,再通运算即可求出结论.本小题也可已建立空间坐标系来求. 在同一球面上,求该球的体积.依题意可得.只要把图形补齐为一个长方体.外接球的直径就是长方体的对角线长.即可求结论.
在同一球面上,求该球的体积.依题意可得.只要把图形补齐为一个长方体.外接球的直径就是长方体的对角线长.即可求结论.
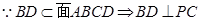 ,
, ,
, 


 则
则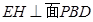 ,
, 为
为 与平面
与平面 所成的角.
所成的角. 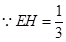 ,
, 则
则
 为底面,
为底面, 为高补成长方体,此时对角线
为高补成长方体,此时对角线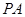 的长为球的直径,
的长为球的直径, ,
,
 .
. 

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源:不详 题型:单选题
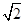 的正方形
的正方形 沿对角线
沿对角线 折起,连结
折起,连结 ,得到三棱锥
,得到三棱锥 ,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )
,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com