
(本小题满分15分)已知函数f(x)=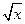 ,g(x)=alnx,a∈R.
,g(x)=alnx,a∈R.
(1)若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2)设函数h(x)=f(x)-g(x),当h(x)存在最小值时,求其最小值φ(a)的解析式;
(3)对(2)中的φ(a),证明:当a∈(0,+∞)时,φ(a)≤1
解:(1)f′(x)=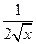 ,g′(x)=
,g′(x)=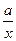 (x>0),
(x>0),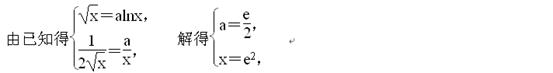
∴两条曲线交点的坐标为(e2,e).切线的斜率为k=f′(e2)=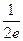 ,
,
∴切线的方程为y-e=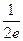 (x-e2).
(x-e2).
(2)由条件知h(x)=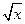 -alnx(x>0),
-alnx(x>0),
∴h′(x)=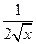 -
-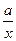 =
=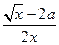 ,
,
①当a>0时,令h′(x)=0,解得x=4a2
∴当0<x<4a2时,h′(x)<0,h(x)在(0,4a2)上单调递减;
当x>4a2时,h′(x)>0, h(x)在(4a2,+∞)上单调递增.
h(x)在(4a2,+∞)上单调递增.
∴x=4a2是h(x)在(0,+∞)上的惟一极值点,且是极小值点,从而也是h(x)的最小值点.
∴最 小值φ(a)=h(4a2)=2a-aln
小值φ(a)=h(4a2)=2a-aln (4a2)=2a[1-ln (2a)].
(4a2)=2a[1-ln (2a)].
解析


科目:高中数学 来源: 题型:解答题
(本小题满分12分) 某厂家拟在2012年举行促销活动,经调查测算,该产品的
某厂家拟在2012年举行促销活动,经调查测算,该产品的
年销售量(即该厂的年产量)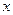 万件与年促销费用
万件与年促销费用 万元(
万元( (
( 为
为
常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2012年生产该产品的
固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格
定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入 两部分资金).
两部分资金).
(Ⅰ) 将2012年该产品的利润y万元表示为年促销费用 万元的函数;
万元的函数;
(Ⅱ) 该厂家2012年的促销费用投入多少万元时,厂家的利 润最大?
润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设函数  ,且其图像相邻的两条对称轴为
,且其图像相邻的两条对称轴为  ,则
,则
A. 的最小正周期为 的最小正周期为  ,且在 ,且在  上为增函数 上为增函数 |
B.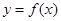 的最小正周期为 的最小正周期为  ,且在 ,且在  上为减函数 上为减函数 |
C.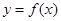 的最小正周期为 的最小正周期为  ,且在 ,且在  上为增函数 上为增函数 |
D.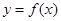 的最小正周期为 的最小正周期为  ,且在 ,且在  上为减函数 上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)已知函数 的图象过点(1, -4),且函数
的图象过点(1, -4),且函数 的图象关于y轴对称.
的图象关于y轴对称.
(1) 求m、n的值及函数 的极值;
的极值;
(2) 求函数 在区间
在区间 上的最大值。
上的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com