
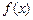 =
=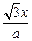 +
+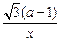 ,a≠0且a≠1.
,a≠0且a≠1.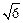 )上单调递减,在(
)上单调递减,在(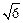 ,
,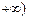 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;科目:高中数学 来源:不详 题型:解答题
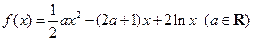 .
.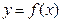 在
在 和
和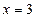 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;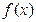 的单调区间;
的单调区间;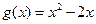 ,若对任意
,若对任意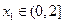 ,均存在
,均存在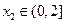 ,使得
,使得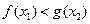 ,求
,求 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (万元)与产量
(万元)与产量 (台)之间的函数关系式是
(台)之间的函数关系式是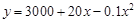
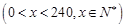 ,若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总体)的最低产量是( )
,若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总体)的最低产量是( )| A.100台 | B.120台 | C.150台 | D.180台 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.{1} | B.{0} |
| C.{0,-1,1} | D.{0,1,2} |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 到实数集
到实数集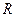 的映射过程:区间
的映射过程:区间 中的实数
中的实数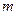 对应数轴上的点
对应数轴上的点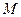 (如图
(如图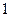 ),将线段
),将线段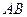 围成一个正方形,使两端点
围成一个正方形,使两端点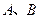 恰好重合(如图
恰好重合(如图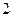 ),再将这个正方形放在平面直角坐标系中,使其中两个顶点在
),再将这个正方形放在平面直角坐标系中,使其中两个顶点在 轴上,点
轴上,点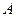 的坐标为
的坐标为 (如图
(如图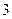 ),若图
),若图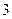 中直线
中直线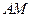 与
与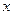 轴交于点
轴交于点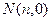 ,则
,则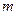 的象就是
的象就是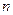 ,记作
,记作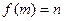 .现给出以下命题:
.现给出以下命题: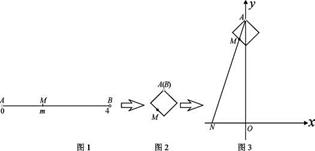
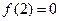 ; ②
; ②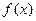 的图象关于点
的图象关于点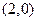 对称;
对称;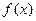 为偶函数; ④
为偶函数; ④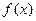 在
在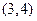 上为常数函数.
上为常数函数.A.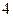 | B.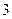 | C.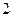 | D.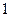 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com