
【题目】已知数列![]() 、
、![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“生成数列”.
的“生成数列”.
(1)若数列![]() 的“生成数列”是
的“生成数列”是![]() ,求
,求![]() ;
;
(2)若![]() 为偶数,且
为偶数,且![]() 的“生成数列”是
的“生成数列”是![]() ,证明:
,证明:![]() 的“生成数列”是
的“生成数列”是![]() ;
;
(3)若![]() 为奇数,且
为奇数,且![]() 的“生成数列”是
的“生成数列”是![]() ,
,![]() 的“生成数列”是
的“生成数列”是![]() ,…,依次将数列
,…,依次将数列![]() ,
,![]() ,
,![]() ,…的第
,…的第![]() 项取出,构成数列
项取出,构成数列![]() .
.
探究:数列![]() 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
试题(1)解:![]() ,
,![]() ,同理,
,同理,![]() ;(2)只需按照定义证明即可,证明:
;(2)只需按照定义证明即可,证明:![]() ,
,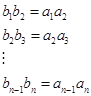 ∵
∵![]() 为偶数,将上述
为偶数,将上述![]() 个等式中第2,4,6, ,
个等式中第2,4,6, ,![]() 这
这![]() 个式子两边取倒数,再将这
个式子两边取倒数,再将这![]() 个式子相乘得:
个式子相乘得:![]()
![]() ,
,![]() 因为
因为![]() ,
,![]() ,所以根据“生成数列”的定义,数列
,所以根据“生成数列”的定义,数列![]() 是数列
是数列![]() 的“生成数列”;(3)因为
的“生成数列”;(3)因为![]() ,所以
,所以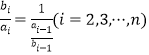 .
.
所以欲证![]() 成等差数列,只需证明
成等差数列,只需证明![]() 成等差数列即可.
成等差数列即可.
试题解析:(1)解:![]() ,
,![]()
同理,![]() . 4分
. 4分
(写对一个![]() 得1分,总分4分)
得1分,总分4分)
(2)证明:![]()
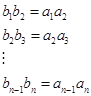 7分
7分
∵![]() 为偶数,将上述
为偶数,将上述![]() 个等式中第2,4,6, ,
个等式中第2,4,6, ,![]() 这
这![]() 个式子两边取倒数,再将这
个式子两边取倒数,再将这![]() 个式子相乘得:
个式子相乘得:![]()
∴![]() 9分
9分
因为![]() ,
,![]()
所以根据“生成数列”的定义,数列![]() 是数列
是数列![]() 的“生成数列”. 10分
的“生成数列”. 10分
(3)证明:因为![]() ,
,
所以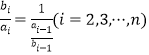 .
.
所以欲证![]() 成等差数列,只需证明
成等差数列,只需证明![]() 成等差数列即可. 12分
成等差数列即可. 12分
对于数列![]() 及其“生成数列”
及其“生成数列”![]()
![]()
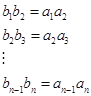
∵![]() 为奇数,将上述
为奇数,将上述![]() 个等式中第2,4,6, ,
个等式中第2,4,6, ,![]() 这
这![]() 个式子两边取倒数,再将这
个式子两边取倒数,再将这![]() 个式子相乘得:
个式子相乘得:
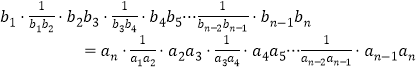
∴![]()
因为![]() ,
,![]()
数列![]() 的“生成数列”为
的“生成数列”为![]() ,因为
,因为![]()
所以![]() 成对比数列.
成对比数列.
同理可证,![]() 也成等比数列.即
也成等比数列.即![]() 是等比数列.
是等比数列.
所以![]() 成等差数列. 16分
成等差数列. 16分


科目:高中数学 来源: 题型:
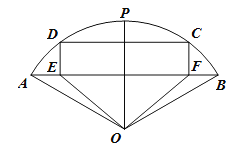
【题目】有一块圆心角为120度,半径为![]() 的扇形钢板
的扇形钢板![]() (
(![]() 为弧
为弧![]() 的中点),现要将其裁剪成一个五边形磨具
的中点),现要将其裁剪成一个五边形磨具![]() ,其下部为等腰三角形
,其下部为等腰三角形![]() ,上部为矩形
,上部为矩形![]() .设
.设![]() 五边形
五边形![]() 的面积为
的面积为![]() .
.
(1)写出![]() 关于
关于![]() 的函数表达式,并写出
的函数表达式,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国高铁的快速发展给群众出行带来巨大便利,极大促进了区域经济社会发展.已知某条高铁线路通车后,发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() ,经测算,高铁的载客量与发车时间间隔
,经测算,高铁的载客量与发车时间间隔![]() 相关:当
相关:当![]() 时高铁为满载状态,载客量为
时高铁为满载状态,载客量为![]() 人;当
人;当![]() 时,载客量会在满载基础上减少,减少的人数与
时,载客量会在满载基础上减少,减少的人数与![]() 成正比,且发车时间间隔为
成正比,且发车时间间隔为![]() 分钟时的载客量为
分钟时的载客量为![]() 人.记发车间隔为
人.记发车间隔为![]() 分钟时,高铁载客量为
分钟时,高铁载客量为![]() .
.
![]() 求
求![]() 的表达式;
的表达式;
![]() 若该线路发车时间间隔为
若该线路发车时间间隔为![]() 分钟时的净收益
分钟时的净收益![]() (元),当发车时间间隔为多少时,单位时间的净收益
(元),当发车时间间隔为多少时,单位时间的净收益![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上钻石的重量计量单位为克拉;已知某种钻石的价值![]() (美元)与其重量
(美元)与其重量![]() (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元;
(1)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若把一颗钻石切割成重量比为![]() 的两颗钻石,求价值损失的百分率;
的两颗钻石,求价值损失的百分率;
(3)把一颗钻石切割成两颗钻石,若两颗钻石的重量分别为![]() 克拉和
克拉和![]() 克拉,试用你所学的数学知识分析当
克拉,试用你所学的数学知识分析当![]() ,
,![]() 满足何种关系时,价值损失的百分率最大.
满足何种关系时,价值损失的百分率最大.
(注:价值损失的百分率![]() ,在切割过程中重量损耗忽略不计)
,在切割过程中重量损耗忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对5年来春节期间服装类商品的优惠金额![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
(单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
日期 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图,并判断服装类商品的优惠金额与销售额是正相关还是负相关;

(2)根据表中提供的数据,求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(3)若2019年春节期间商场预定的服装类商品的优惠金额为10万元,估计该商场服装类商品的销售额.
参考公式:
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l方程为(m+2)x﹣(m+1)y﹣3m﹣7=0,m∈R.
(1)求证:直线l恒过定点P,并求出定点P的坐标;
(2)若直线l在x轴,y轴上的截距相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M与直线![]() 相切于点
相切于点![]() ,圆心M在x轴上.
,圆心M在x轴上.
(1)求圆M的方程;
(2)过点M且不与x轴重合的直线与圆M相交于A,B两点,O为坐标原点,直线OA,OB分别与直线x=8相交于C,D两点,记△OAB、△OCD的面积分别是S1、S2.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com