Question

对于函数y＝f(x)(x∈D，D是此函数的定义域)若同时满足下列条件：

(Ⅰ)f(x)在D内单调递增或单调递减；

(Ⅱ)存在区间[a，b]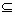D，使f(x)在[a，b]上的值域为[a，b]；那么，把y＝f(x)(x∈D)叫闭函数．

(1)求闭函数y＝－x³符合条件(Ⅱ)的区间[a，b]；

(2)判断函数f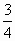(x)＝x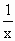＋(x∈R⁺)是否为闭函数？并说明理由；

(3)若y＝k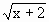＋是闭函数，求实数k的取值范围．

Answer 1

答案：
解析：

解：(1)易知y＝－x3为[a，b]上的减函数　　∴ 　　注意到a＞b，可得 　　∴所求的区间为[－1，1] 　　(2)取x1＝1，x2＝10，则f(x1)＝＜＝f(x2) 　　故f(x)不是(0，＋∞)上的减函数 　　取x1＝，x2＝，则f(x1)＝＋10＜＋1000＝f(x2) 　　故f(x)不是(0，＋∞)上的增函数 　　∴f(x)不是闭函数 　　(3)设函数y＝k＋符合条件(Ⅱ)的区间为[a，b] 　　则 　　∴a，b为方程x＝k＋的两实根 　　∴命题等价于关于x的方程 　　上有两不等实根 　　当k≤－2时　　∴k＞－ 　　∴－＜k≤－2 　　当k＞－2时　　－＜k≤－2不合题意 　　∴k的取值范围为(－，－2] 　　注：(1)Ⅲ用数形结合法酌情给分 　　(2)(Ⅱ)(文)只要说明f(x)不是R+上的单调函数易给出f(x)不是闭函数的结论可给满分．