[题目]曲线y＝1+ 与直线y＝k(x-2)+4有两个交点.则实数k的取值范围是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】曲线y＝1＋与直线y＝k（x－2）＋4有两个交点，则实数k的取值范围是（）
A.
B.
C.
D.

【答案】D
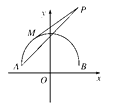
【解析】由y＝1＋得x2＋（y－1）2＝4（y≥1），表示如图所示半圆．直线y＝k（x－2）＋4恒过点（2,4）．设A（－2,1），B（2,1），P（2,4）．直线MP与半圆相切，直线MP的方程为，即，圆心到直线MP的距离为，解得，又kPA＝，∴ .

所以答案是：D。
【考点精析】掌握圆的一般方程是解答本题的根本，需要知道圆的一般方程的特点：(1)①x2和y2的系数相同，不等于0．②没有xy这样的二次项；(2)圆的一般方程中有三个特定的系数D、E、F，因之只要求出这三个系数，圆的方程就确定了；(3)、与圆的标准方程相比较，它是一种特殊的二元二次方程，代数特征明显，圆的标准方程则指出了圆心坐标与半径大小，几何特征较明显．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某省高考改革新方案，不分文理科，高考成绩实行“3+3”的构成模式，第一个“3”是语文、数学、外语，每门满分150分，第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试，每门满分100分，高考录取成绩卷面总分满分750分．为了调查学生对物理、化学、生物的选考情况，将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S，从学生群体S中随机抽取了50名学生进行调查，他们选考物理，化学，生物的科目数及人数统计如表：

选考物理、化学、生物的科目数	1	2	3
人数	5	25	20

（I）从所调查的50名学生中任选2名，求他们选考物理、化学、生物科目数量不相等的概率；
（II）从所调查的50名学生中任选2名，记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值，求随机变量X的分布列和数学期望；
（III）将频率视为概率，现从学生群体S中随机抽取4名学生，记其中恰好选考物理、化学、生物中的两科目的学生数记作Y，求事件“y≥2”的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】定义为n个正数p1 ， p2 ， …，pn的“均倒数”．若已知正数数列{an}的前n项的“均倒数”为，又bn= ，则 + + +…+ =（）
A.
B.
C.
D.