练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．计算（$\root{3}{2}$）6-$\frac{7}{5}$×（$\frac{49}{25}$）${\;}^{-\frac{1}{2}}$-lg$\frac{1}{10}$=4．

    分析 根据指数幂的运算性质计算即可．

    解答 解：（$\root{3}{2}$）6-$\frac{7}{5}$×（$\frac{49}{25}$）${\;}^{-\frac{1}{2}}$-lg$\frac{1}{10}$=${2}^{\frac{1}{3}×6}$-$\frac{7}{5}$×$\frac{5}{7}$+1=4-1+1=4，
    故答案为：4．

    点评 本题考查了指数幂的运算性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届江苏南通市如东县等高三10月联考数学试卷（解析版） 题型：解答题

    给出定义在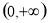上的两个函数,.

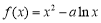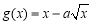    （1）若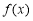在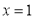处取最值．求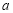的值；

    （2）若函数在区间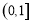上单调递减，求实数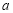的取值范围；

    （3）试确定函数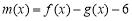的零点个数，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若f（x）=$\left\{\begin{array}{l}{f（x-5），x＞0}\\{{2}^{x+2}{+∫}_{0}^{\frac{π}{6}}cos3tdt，x≤0}\end{array}\right.$，则f（2017）=（　　）
    A．$\frac{1}{3}$B．$\frac{1}{6}$C．$\frac{5}{6}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=x2-x+ce-2x（c∈R）．
    （1）若f（x）是在定义域内的增函数，求c的取值范围；
    （2）若函数F（x）=f（x）+f'（x）-$\frac{5}{2}$（其中f'（x）为f（x）的导函数）存在三个零点，求c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列各组对象不能构成一个集合的是（　　）
    A．不超过20的非负实数
    B．方程x2-9=0在实数范围内的解
    C．$\sqrt{3}$的近似值的全体
    D．临川十中2016年在校身高超过170厘米的同学的全体

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，且满足f（0）=f（$\frac{π}{3}$）则下列说法正确的是（　　）
    A．f（x）的最小正周期为2πB．f（x）在[0，$\frac{π}{4}$]上是增函数
    C．f（x）的图象关于直线x=$\frac{5}{6}$π对称D．f（$\frac{2π}{3}$）=-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．定义在R上的函数f（x）满足（x-1）f′（x）≤0，且f（-x）=f（2+x），当|x1-1|＜|x2-1|时，有（　　）
    A．f（2-x1）≥f（2-x2）B．f（2-x1）=f（2-x2）C．f（2-x1）＞f（2-x2）D．f（2-x1）≤f（2-x2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数y=f（x）是R上的偶函数，且在（-∞，0]上是增函数，若f（a）≤f（2），则实数a的取值范围是（　　）
    A．a≤2B．a≥-2C．a≤-2或 a≥2D．-2≤a≤2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．计算：（2$\frac{1}{4}$）${\;}^{\frac{1}{2}}}$-（-2016）0-（$\frac{27}{8}$）${\;}^{-\frac{2}{3}}}$+（$\frac{3}{2}$）-2．

    查看答案和解析>>

    同步练习册答案