
根据我国发布的《环境空气质量指数 技术规定》 (试行),
技术规定》 (试行), 共分为六级:
共分为六级: 为优,
为优, 为良,
为良, 为轻度污染,
为轻度污染, 为中度污染,
为中度污染, ,
, 均为重度污染,
均为重度污染, 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份 天的
天的 的频率分布直方图如图所示:
的频率分布直方图如图所示:

(1)该市11月份环境空气质量优或良的共有多少天?
(2)若采用分层抽样方法从 天中抽取
天中抽取 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
(3)空气质量指数低于 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
⑴6;⑵3;⑶0.6.
【解析】
试题分析:(1)由题意知样本容量为30,由频率分布直方图求出环境空气质量优或良的概率,可求得11月份环境空气质量优或良的天数;(2)求出中度污染的概率,算出11月份30天中中度污染的天数,进而可求中度污染被抽到的天数;(3)空气质量指数低于150的,在频率分布直方图中有三个小矩形,求出前三个小矩形的面积和即可.
试题解析:(1)∵11月份共30天,∴由题意知样本容量为30.
∵环境空气质量优或良的概率为(0.002+0.002)×50=0.2,
∴该市11月份环境空气质量优或良的共有0.2×30=6天.
(2)∵中度污染的概率为0.006×50=0.3,∴11月份30天中由9天是中度污染.
又每一天被抽到的概率相等,∴抽取10天,中度污染被抽到的天数共有0.3×10=3天.
(3)设“市民王先生当天适宜户外晨练”为事件A,则 .
.
考点:1、古典概型及其概率计算公式;2、频率分布直方图;3、分层抽样.


科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:解答题
已知椭圆 :
: 的离心率为
的离心率为 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.

(1)求椭圆 的方程;
的方程;
(2)如图,设椭圆 的上、下顶点分别为
的上、下顶点分别为 ,
,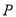 是椭圆上异于
是椭圆上异于 的任意一点,直线
的任意一点,直线 分别交
分别交 轴于点
轴于点 ,若直线
,若直线 与过点
与过点 的圆
的圆 相切,切点为
相切,切点为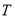 .证明:线段
.证明:线段 的长为定值.
的长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com