
设函数 ,曲线
,曲线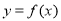 在点(1,
在点(1,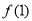 处的切线为
处的切线为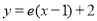 . (Ⅰ)求
. (Ⅰ)求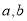 ;
;
(Ⅱ)证明: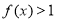 .
.
(Ⅰ)a=1,b=2;(Ⅱ)祥见解析.
【解析】
试题分析:(Ⅰ)由曲线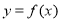 在点(1,
在点(1,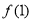 处的切线为
处的切线为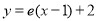 可知
可知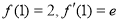 ,求出函数
,求出函数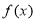 的导函数,可得到关于a,b的一个二元方程组,解之即可得到a,b的值;(Ⅱ)由(Ⅰ)得
的导函数,可得到关于a,b的一个二元方程组,解之即可得到a,b的值;(Ⅱ)由(Ⅰ)得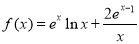 ,从而
,从而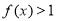 等价于
等价于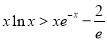 ;在
;在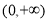 分别利用导数求函数
分别利用导数求函数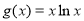 的最小值,和函数
的最小值,和函数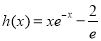 的最大值;从而就可证明不等式
的最大值;从而就可证明不等式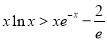 成立,即
成立,即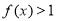 成立.
成立.
试题解析:(Ⅰ)由已知得:函数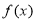 的定义域为
的定义域为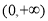 ,
,
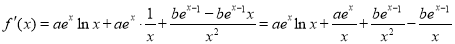 ;
;
由题意可得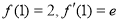 ,即
,即
故有a=1,b=2;
(Ⅱ)由(Ⅰ)知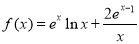 ,从而
,从而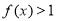 等价于
等价于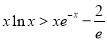 ;
;
设函数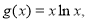 则
则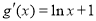 ;
;
所以当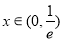 时,
时,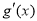 <0;当
<0;当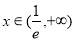 时,
时, 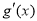 >0.
>0.
故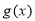 在
在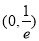 上单调递减,在
上单调递减,在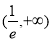 上单调递增,从而
上单调递增,从而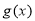 在(0,+
在(0,+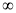 )上的最小值为
)上的最小值为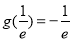 .
.
设函数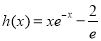 ,则
,则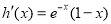 ;
;
所以当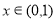 时
时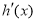 >0;当
>0;当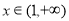 时,
时,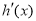 <0.
<0.
故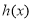 在
在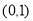 上单调递增,在
上单调递增,在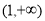 上单调递减,从而
上单调递减,从而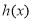 在(0,+
在(0,+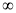 )上的最大值为
)上的最大值为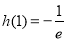 .
.
综上得:当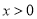 时,恒有
时,恒有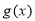 >
>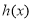 ,即
,即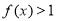 .
.
考点:1.导数的几何意义;2.利用导数证明不等式.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:解答题
如图,在长方体 中,
中,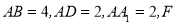 是棱
是棱 的中点,点
的中点,点 在棱
在棱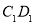 上,且
上,且 (
( 为实数).
为实数).
(1)当 时,求直线
时,求直线 与平面
与平面 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)试问:直线 与直线
与直线 能否垂直?请说明理由.
能否垂直?请说明理由.

查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB?平面CMN.

查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:解答题
根据我国发布的《环境空气质量指数 技术规定》 (试行),
技术规定》 (试行), 共分为六级:
共分为六级: 为优,
为优, 为良,
为良, 为轻度污染,
为轻度污染, 为中度污染,
为中度污染, ,
, 均为重度污染,
均为重度污染, 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份 天的
天的 的频率分布直方图如图所示:
的频率分布直方图如图所示:

(1)该市11月份环境空气质量优或良的共有多少天?
(2)若采用分层抽样方法从 天中抽取
天中抽取 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
(3)空气质量指数低于 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com