
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB?平面CMN.

(1)详见解析,(2)详见解析.
【解析】
试题分析:(1)证明线面平行,需先证明线线平行.证明线线平行,需先利用平行四边形. 取A1C1的中点P,则可得四边形AMNP为平行四边形,所以MN∥AP.因为AP?平面AA1C1C,MN?平面AA1C1C,所以MN∥平面AA1C1C.(2)条件中面面垂直,需先化为线面垂直. 因为平面CC1B1B⊥平面ABC,平面CC1B1B∩平面ABC=BC.CN?平面CC1B1B,CN?BC,所以CN⊥平面ABC.因为AB?平面ABC,所以CN⊥AB.因为CM?平面CMN,CN?平面CMN,CM∩CN=C,所以AB⊥平面CMN.
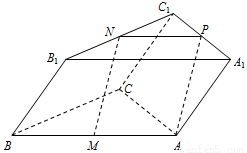
试题解析:证明:(1)取A1C1的中点P,连接AP,NP.
因为C1N=NB1,C1P=PA1,所以NP∥A1B1,NP=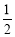 A1B1. 2分
A1B1. 2分
在三棱柱ABC-A1B1C1中,A1B1∥AB,A1B1=AB.
故NP∥AB,且NP=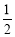 AB.
AB.
因为M为AB的中点,所以AM=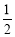 AB.
AB.
所以NP=AM,且NP∥AM.
所以四边形AMNP为平行四边形.
所以MN∥AP. 4分
因为AP?平面AA1C1C,MN?平面AA1C1C,
所以MN∥平面AA1C1C. 6分
(2)因为CA=CB,M为AB的中点,所以CM⊥AB. 8分
因为CC1=CB1,N为B1C1的中点,所以CN⊥B1C1.
在三棱柱ABC-A1B1C1中,BC∥B1C1,所以CN?BC.
因为平面CC1B1B⊥平面ABC,平面CC1B1B∩平面ABC=BC.CN?平面CC1B1B,
所以CN⊥平面ABC. 10分
因为AB?平面ABC,所以CN⊥AB. 12分
因为CM?平面CMN,CN?平面CMN,CM∩CN=C,
所以AB⊥平面CMN. 14分
考点:线面平行判定定理,面面垂直性质定理,线面垂直判定定理


科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
如图,PA是圆O的切线,A为切点,PO与圆O交于点B、C,AQ?OP,垂足为Q.若PA=4,PC=2,求AQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com