
如图,PA是圆O的切线,A为切点,PO与圆O交于点B、C,AQ?OP,垂足为Q.若PA=4,PC=2,求AQ的长.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届江苏省高二第二学期阶段测试文科数学试卷(解析版) 题型:解答题
定义在[﹣1,1]上的奇函数f(x)满足f(1)=2,且当a,b∈[﹣1,1],a+b≠0时,有 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:解答题
如图,在长方体 中,
中,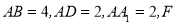 是棱
是棱 的中点,点
的中点,点 在棱
在棱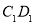 上,且
上,且 (
( 为实数).
为实数).
(1)当 时,求直线
时,求直线 与平面
与平面 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)试问:直线 与直线
与直线 能否垂直?请说明理由.
能否垂直?请说明理由.

查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
某商店为了吸引顾客,设计了一个摸球小游戏,顾客从装有1个红球,1个白球,3个黑球的袋中一次随机的摸2个球,设计奖励方式如下表:
结果 | 奖励 |
1红1白 | 10元 |
1红1黑 | 5元 |
2黑 | 2元 |
1白1黑 | 不获奖 |
(1)某顾客在一次摸球中获得奖励X元,求X的概率分布表与数学期望;
(2)某顾客参与两次摸球,求他能中奖的概率.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB?平面CMN.

查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试文科数学试卷(解析版) 题型:填空题
记数列{an}的前n项和为Sn.若a1=1,Sn=2(a1+an)(n≥2,n∈N*),则Sn= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com