
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,其中
,其中![]() .证明:
.证明:![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.
【答案】(1) ![]() .
.
(2) ![]() .
.
(3)证明见解析.
【解析】分析:(Ⅰ)求出函数的导数,计算![]() 和
和![]() 的值,点斜式求出切线方程即可.
的值,点斜式求出切线方程即可.
(Ⅱ)设![]() ,并求导.将问题转化为在区间
,并求导.将问题转化为在区间![]() 上,
上,![]() 恒成立,或者
恒成立,或者![]() 恒成立,通过特殊值
恒成立,通过特殊值![]() ,且
,且![]() ,确定
,确定![]() 恒成立,通过参数分离,求得实数
恒成立,通过参数分离,求得实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,将问题转化为证明
,将问题转化为证明![]() ,利用函数的导数确定函数最小值
,利用函数的导数确定函数最小值![]() 在区间
在区间![]() ,并证明
,并证明![]() . 即
. 即![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.
详解:解:(Ⅰ)求导,得![]() ,
,
又因为![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)设函数![]() ,
,
求导,得![]() ,
,
因为函数![]() 在区间
在区间![]() 上为单调函数,
上为单调函数,
所以在区间![]() 上,
上,![]() 恒成立,或者
恒成立,或者![]() 恒成立,
恒成立,
又因为![]() ,且
,且![]() ,
,
所以在区间![]() ,只能是
,只能是![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
又因为函数![]() 在在区间
在在区间![]() 上单调递减,
上单调递减,![]() ,
,
所以![]() .
.
(Ⅲ)证明:设![]() .
.
求导,得![]() .
.
设![]() ,则
,则![]() (其中
(其中![]() ).
).
所以当![]() 时,
时,![]() (即
(即![]() )为增函数.
)为增函数.
又因为![]() ,
,
所以,存在唯一的![]() ,使得
,使得![]()
且![]() 与
与![]() 在区间
在区间![]() 上的情况如下:
上的情况如下:
|
|
|
|
| - | 0 | + |
| ↘ |
| ↗ |
所以,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]()
![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() 的图象在
的图象在![]() 图象的下方.
图象的下方.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围;
(2)当b=1时,若对任意x∈[0,1],-1≤f(x)≤1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥![]() 的底面是正六边形,
的底面是正六边形,![]() 平面
平面![]() ,
,![]() ,给出下列结论:
,给出下列结论:
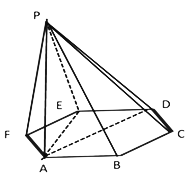
①![]() ;
;
②直线![]() 平面
平面![]() ;
;
③平面![]() 平面
平面![]() ;
;
④异面直线![]() 与
与![]() 所成角为
所成角为![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
其中正确的有_______(把所有正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个产品有若千零部件构成,加工时需要经过6道工序,分别记为![]() .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序![]() 必须要在工序
必须要在工序![]() 完成后才能开工,则称
完成后才能开工,则称![]() 为
为![]() 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
工序 |
|
|
|
|
|
|
加工时间 | 3 | 4 | 2 | 2 | 2 | 1 |
紧前工序 | 无 |
| 无 |
|
|
|
现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是__________小时.(假定每道工序只能安排在一台机器上,且不能间断).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心![]() 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心![]() 位于
位于![]() 轴正半轴上,与直线
轴正半轴上,与直线![]() 相切且被轴
相切且被轴![]() 截得的弦长为
截得的弦长为![]() ,圆
,圆![]() 的面积小于13.
的面积小于13.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,以
,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在这样的直线
.是否存在这样的直线![]() ,使得直线
,使得直线![]() 与
与![]() 恰好平行?如果存在,求出
恰好平行?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为
为![]() 椭圆上一点,且
椭圆上一点,且![]() 垂直于
垂直于![]() 轴,连结
轴,连结![]() 并延长交椭圆于另一点
并延长交椭圆于另一点![]() ,设
,设![]() .
.
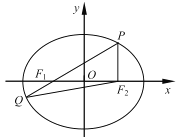
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程及
的方程及![]() 的值;
的值;
(2)若![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围.
的离心率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com