考点:椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:由已知条件推导出曲线C
2:y
2=4x.
=(x1-1,y1-2),
=(x2-x1,y2-y1),由AB⊥BC,推导出
y12+(2+y2)y1+(2y2+16)=0,由此能求出y
2 的取值范围.
解答:解:∵椭圆C
1:
+
=1的左右焦点为F
1,F
2,
∴F
1(-1,0),F
2(1,0),直线l
1:x=-1,
设l
2:y=t,设P(-1,t),(t∈R),M(x,y),
则y=t,且由|MP|=|MF
2|,
∴(x+1)
2=(x-1)
2+y
2,
∴曲线C
2:y
2=4x.
∵A(1,2),B(x
1,y
1),C(x
2,y
2)是C
2上不同的点,
∴
=(x1-1,y1-2),
=(x2-x1,y2-y1),
∵AB⊥BC,
∴
•=(x
1-1)(x
2-x
1)+(y
1-2)(y
2-y
1)=0,
∵
x1=y12,
x2=y22,
∴(
y12-4)(
y22-
y12)+
=0,
∵y
1≠2,y
1≠y
2,
∴
+1=0,
整理,得
y12+(2+y2)y1+(2y2+16)=0,
关于y
1的方程有不为2的解,
∴
△=(2+y2)2-4(2y2+16)≥0,且y
2≠-6,
∴
y22-4y2-60≥0,且y
2≠-6,
解得y
2<-6,或y
2 ≥10.
故选:A.
点评:本题考查实数的取值范围的求法,综合性强,难度大,解题时要熟练掌握圆锥曲线的简单性质,注意函数与方程思想的合理运用.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案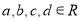 ,函数
,函数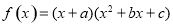 ,
,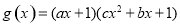 ,集合
,集合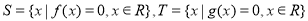 ,记
,记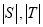 分别为集合
分别为集合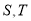 中元素的个数,那么下列结论不可能的是
中元素的个数,那么下列结论不可能的是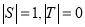 B.
B.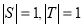
 D.
D.