
 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.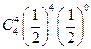 =
=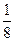 .……………..2分
.……………..2分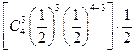 =
=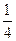 ,…………….4分
,…………….4分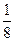 +
+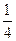 ]=
]=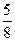 .…………….6分
.…………….6分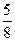 .
. (ξ=6)=2
(ξ=6)=2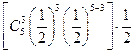 =
=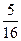 ,………………..8分
,………………..8分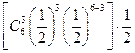 =
=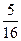 ,………………..10分
,………………..10分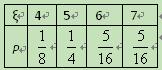 ………………………………………………………
……………………………………………………… ..12分[
..12分[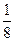 +5·
+5·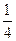 +6·
+6·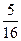 +7·
+7·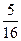
 =
=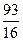 .……………14分
.……………14分

科目:高中数学 来源:不详 题型:解答题
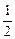 .记小球遇到第
.记小球遇到第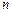 行第
行第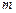 个障碍物(从左至右)上顶点的概率为
个障碍物(从左至右)上顶点的概率为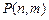 .
.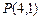 ,
,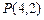 的值,并猜想
的值,并猜想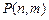 的表达式(不必证明);
的表达式(不必证明);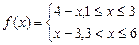 ,设小球遇到第6行第
,设小球遇到第6行第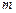 个障碍物(从左至右)上顶点时,
个障碍物(从左至右)上顶点时,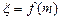 ,试求
,试求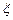 的分布列及数学期望.
的分布列及数学期望.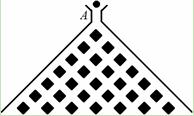
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 学历 | 35岁以下 | 35~50岁 | 50岁以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 |  | 20 |  |
 个人,其中35岁以下抽
个人,其中35岁以下抽 个人中随机抽取出1人,此人的年龄为50岁以上
个人中随机抽取出1人,此人的年龄为50岁以上 ,求
,求 、
、 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
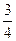 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是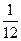 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是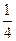 ;
;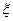 表示回答该题对的人数,求
表示回答该题对的人数,求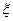 的分布列和
的分布列和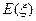 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com