[题目]中国古代数学名著中有这样一个问题:今有牛.马.羊食人苗.苗主责之粟五斗.羊主曰:“我羊食半马．马主曰:“我马食半牛．今欲衰偿之.问各出几何?此问题的译文是:今有牛.马.羊吃了别人的禾苗.禾苗主人要求赔偿5斗粟．羊主人说:“我羊所吃的禾苗只有马的一半．马主人说:“我马所吃的禾苗只有牛的一半．打算按此比例偿还.他门各应偿还多少?该问题中.1 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】中国古代数学名著《九章算术》中有这样一个问题：今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰：“我羊食半马．”马主曰：“我马食半牛．”今欲衰偿之，问各出几何？此问题的译文是：今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟．羊主人说：“我羊所吃的禾苗只有马的一半．”马主人说：“我马所吃的禾苗只有牛的一半．”打算按此比例偿还，他门各应偿还多少？该问题中，1斗为10升，则羊主人应偿还多少升粟？（）

A.B.C.D.

【答案】C

【解析】

设牛、马、羊所吃禾苗分别为，，，是公比为的等比数列，根据等比数列的求和公式求出首项，再根据等比数列的通项公式即可求解.

设牛、马、羊所吃禾苗分别为，，，

则是公比为的等比数列，∴，

解得，∴羊主人应偿还：升粟．

故选：C．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面为矩形，已知平面，为的中点，，过点作于，连接，，.

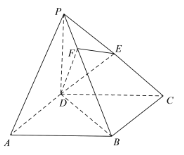
（1）求证：平面平面；

（2）若直线与平面所成角的正切值为，求平面与平面所成锐二面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为（2，0），（），圆C的参数方程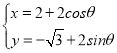（θ为参数）．

（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；

（Ⅱ）判断直线l与圆C的位置关系．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知曲线C的极坐标方程为，直线l的参数方程为（为参数，0≤α＜π）．

（1）求曲线C的直角坐标方程．并说明曲线C的形状；

（2）若直线l经过点M（1，0）且与曲线C交于A、B两点，求|AB|．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某艺术品公司欲生产一款迎新春工艺礼品，该礼品是由玻璃球面和该球的内接圆锥组成，圆锥的侧面用于艺术装饰，如图1.为了便于设计，可将该礼品看成是由圆O及其内接等腰三角形绕底边上的高所在直线旋转而成，如图2.已知圆O的半径为，设，，圆锥的侧面积为（S圆锥的侧面积（R-底面圆半径，I-母线长））

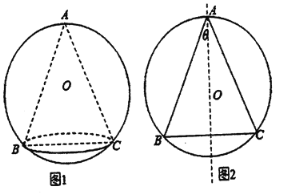
（1）求S关于的函数关系式；

（2）为了达到最佳观赏效果，要求圆锥的侧面积S最大.求S取得最大值时腰的长度

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在直三棱柱中，已知，，，.是线段的中点.

（1）求直线与平面所成角的正弦值；

（2）求二面角的大小的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某游戏公司对今年新开发的一些游戏进行评测，为了了解玩家对游戏的体验感，研究人员随机调查了300名玩家，对他们的游戏体验感进行测评，并将所得数据统计如图所示，其中.

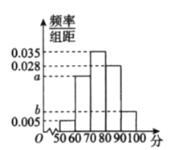
（1）求这300名玩家测评分数的平均数；

（2）由于该公司近年来生产的游戏体验感较差，公司计划聘请3位游戏专家对游戏进行初测，如果3人中有2人或3人认为游戏需要改进，则公司将回收该款游戏进行改进；若3人中仅1人认为游戏需要改进，则公司将另外聘请2位专家二测，二测时，2人中至少有1人认为游戏需要改进的话，公司则将对该款游戏进行回收改进.已知该公司每款游戏被每位专家认为需要改进的概率为，且每款游戏之间改进与否相互独立.