
【题目】已知圆![]() 和焦点为F的抛物线
和焦点为F的抛物线![]() 上一点,M是
上一点,M是![]() 上,当点M在
上,当点M在![]() 时,
时,![]() 取得最小值,当点M在
取得最小值,当点M在![]() 时,
时,![]() 取得最大值,则
取得最大值,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他门各应偿还多少?该问题中,1斗为10升,则羊主人应偿还多少升粟?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行象棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() )的焦点F且斜率为
)的焦点F且斜率为![]() 的直线交抛物线C于M,N两点,且
的直线交抛物线C于M,N两点,且![]() .
.
(1)求p的值;
(2)抛物线C上一点![]() ,直线
,直线![]() (其中
(其中![]() )与抛物线C交于A,B两个不同的点(A,B均与点Q不重合).设直线QA,QB的斜率分别为
)与抛物线C交于A,B两个不同的点(A,B均与点Q不重合).设直线QA,QB的斜率分别为![]() ,
,![]() .直线l是否过定点?如果是,请求出所有定点;如果不是,请说明理由;
.直线l是否过定点?如果是,请求出所有定点;如果不是,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某个机械零件是由两个有公共底面的圆锥组成的,且这两个圆锥有公共点的母线互相垂直,把这个机械零件打磨成球形,该球的半径最大为1,设这两个圆锥的高分别为![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)(x∈R)满足f(1+x)=f(1-x)且x∈[-1,1]时,f(x)=1-x2,函数g(x)=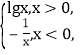 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com