
(12分)如图,在四棱锥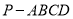 中,底面
中,底面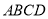 是矩形,已知
是矩形,已知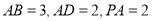 ,
,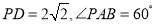
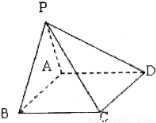
(1)证明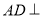 平面
平面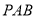 ;
;
(2)求异面直线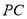 与
与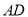 所成的角的正切值;
所成的角的正切值;
(3)求四棱锥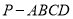 的体积。
的体积。
(1)证明见解析,(2)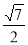 ,(3)
,(3)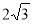 ,
,
【解析】
试题分析:首先要证明线面垂直,只需寻求线线垂直,已知底面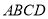 是矩形
是矩形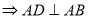 ,在
,在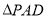 中,
中,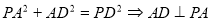 ,得出
,得出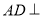 平面
平面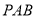 ;第二步由于
;第二步由于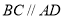 ,异面直线
,异面直线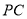 与
与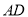 所成的角就是
所成的角就是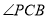 ,在
,在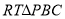 中求出
中求出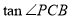 即可;第三步由
即可;第三步由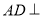 平面
平面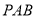 ,又
,又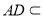 平面
平面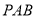 ,则平面
,则平面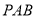
 平面
平面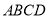 ,过点
,过点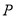 作
作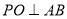 ,垂足为
,垂足为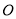 ,则
,则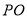
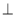 平面
平面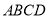 ,求出棱锥的高
,求出棱锥的高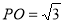 ,在求出体积;
,在求出体积;
试题解析:(1)由已知底面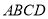 是矩形
是矩形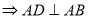 ,在
,在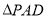 中,
中,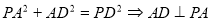 ,又
,又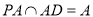 ,则
,则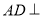 平面
平面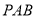 ;
;
(2)由于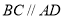 ,异面直线
,异面直线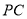 与
与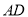 所成的角就是
所成的角就是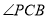 ,由于
,由于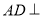 平面
平面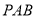 ,则
,则
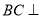 平面
平面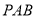 ,又
,又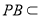 平面
平面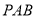 ,则
,则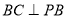 ,在
,在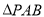 中,
中,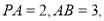
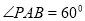 ,则
,则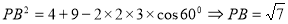 ,在
,在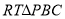 中,
中,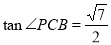 ;
;
(3)由(1)知,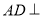 平面
平面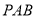 ,又
,又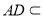 平面
平面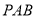 ,则平面
,则平面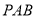
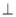 平面
平面 ,过点
,过点 作
作 ,垂足为
,垂足为 ,则
,则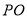
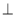 平面
平面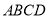 ,
,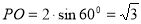 ,四棱锥
,四棱锥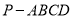 的体积
的体积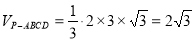 .
.
考点:1.直线与平面垂直的判定和性质;2.异面直线所成的角;3..面面垂直的性质定理;4.棱锥的体积;


科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.1随机对照实验案例练习卷(解析版) 题型:?????
某学校准备调查高三年级学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机对24名同学进行调查;第二种由教务处对年级的240名学生编号,由001到240,请学号最后一位为3的同学参加调查,则这两种抽样方式依次为( )
A.分层抽样,简单随机抽样 B.简单随机抽样,分层抽样
C.分层抽样,系统抽样 D.简单随机抽样,系统抽样
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修四 9.4分期付款问题中的有关计算练习卷(解析版) 题型:?????
(2013•烟台一模)已知数列{an}(n∈N*)是各项均为正数且公比不等于1的等比数列,对于函数y=f(x),若数列{1nf(an)}为等差数列,则称函数f(x)为“保比差数列函数”.现有定义在(0,+∞)上的三个函数:①f(x)= ;②f(x)=ex ③f(x)=
;②f(x)=ex ③f(x)=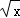 ,则为“保比差数列函数”的是( )
,则为“保比差数列函数”的是( )
A.①② B.②③ C.①③ D.①②③
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.4几何问题的代数解法练习卷(解析版) 题型:?????
(2014•凉山州二模)若顶点在原点,始边为x轴的非负半轴的钝角α的终边与圆x2+y2=2相交于A(x1,y1),射线OA绕点O顺时针旋转30°后,与圆x2+y2=2相交于B(x2,y2),当|x1﹣x2|有最大值时,cosα=( )
A.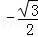 B.
B.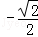 C.
C.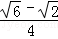 D.
D.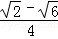
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.4几何问题的代数解法练习卷(解析版) 题型:?????
(2014•茂名一模)已知直线l1:ax+2y+1=0与直线l2:(3﹣a)x﹣y+a=0,若l1∥l2,则a的值为( )
A.1 B.2 C.6 D.1或2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省大同市高二上学期期中考试文科数学试卷(解析版) 题型:填空题
以点A(1,4),B(3,-2)为直径的两个端点的圆的一般式方程为___________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省大同市高二上学期期中考试文科数学试卷(解析版) 题型:解答题
如图,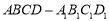 为正方体,下面结论错误的是
为正方体,下面结论错误的是
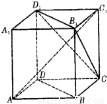
A. 平面
平面
B.
C.平面ACC1A1⊥平面
D.异面直线 与
与 所成的角为60°
所成的角为60°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高二上学期1月质量检测数学试卷(解析版) 题型:填空题
双曲线的中心在原点,焦点在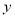 轴上,焦距为16,一条渐近线方程为
轴上,焦距为16,一条渐近线方程为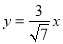 ,则双曲线方程为
,则双曲线方程为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com