
【题目】如图甲,四边形![]() 中,
中,![]() 是
是![]() 的中点,
的中点, ![]() .将(图甲)沿直线
.将(图甲)沿直线![]() 折起,使二面角
折起,使二面角![]() 为
为![]() (如图乙).
(如图乙).
(1)求证:![]() ⊥平面
⊥平面![]()
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
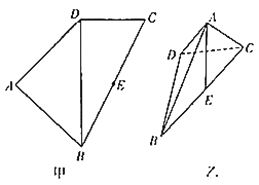
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,可知
,可知![]() ,
,![]() 平面
平面![]() ,即
,即![]() ,也可证明
,也可证明![]() ,根据线面垂直的判断定理可证
,根据线面垂直的判断定理可证![]() 平面
平面![]() ;(2)根据等体积转化
;(2)根据等体积转化![]() ,可得点到平面的距离,或是利用空间直角坐标解决.
,可得点到平面的距离,或是利用空间直角坐标解决.
试题解析:(Ⅰ)证明:如图,取BD中点M,连接AM,ME.
![]()
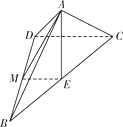
因为AB=AD=![]() ,所以AM⊥BD, 因为DB=2,DC=1,BC=
,所以AM⊥BD, 因为DB=2,DC=1,BC=![]() ,满足:DB 2+DC 2=BC 2, 所以△BCD是以BC为斜边的直角三角形,BD⊥DC,因为E是BC的中点,所以ME为△BCD的中位线,
,满足:DB 2+DC 2=BC 2, 所以△BCD是以BC为斜边的直角三角形,BD⊥DC,因为E是BC的中点,所以ME为△BCD的中位线,![]() ME∥
ME∥![]() ,
,![]() ME⊥BD,ME=
ME⊥BD,ME=![]()
![]() ∠AME是二面角A-BD-C的平面角,
∠AME是二面角A-BD-C的平面角,![]() =
=![]() °.
°.
![]() ,
,![]() 且AM、ME是平面AME内两条相交于点M的直线,
且AM、ME是平面AME内两条相交于点M的直线,
![]() ,
,![]() 平面AEM,
平面AEM,![]() .
.
![]() ,
,![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,在△AME中,由余弦定理得:
,在△AME中,由余弦定理得:
![]()
![]()
![]() ,
,![]() .
.
(Ⅱ)解法一:等体积法.
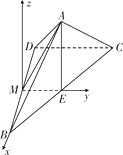
解法二:如图5,以M为原点,MB所在直线为x轴,ME所在直线为y轴,
平行于EA的直线为z轴,建立空间直角坐标系,
则由(Ⅰ)及已知条件可知B(1,0,0),![]() ,
,![]() ,D
,D![]() ,C
,C![]() .则
.则![]()
![]() 设平面ACD的法向量为
设平面ACD的法向量为![]() =
=![]() ,
,
则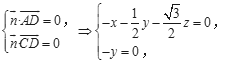 令
令![]() 则z=-2,
则z=-2,![]()
![]() 到平面
到平面![]() 的距离为d,则
的距离为d,则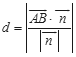 ,所以d
,所以d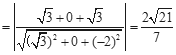 .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P点到两定点D(﹣2,0),E(2,0)连线斜率之积为- ![]() .
.
(1)求证:动点P恒在一个定椭圆C上运动;
(2)过 ![]() 的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为 ![]() .
. 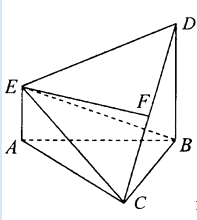
(1)若F是线段CD的中点,证明:EF⊥平面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[(g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,则g(x)的解析式为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为某几何体形状的纸盒的三视图,在此纸盒内放一个小正四面体,若小正四面体在纸盒内可以任意转动,则小正四面体的棱长的最大值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系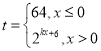 且该食品在4℃的保鲜时间是16小时.
且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示.给出以下四个结论:

①该食品在6℃的保鲜时间是8小时;
②当x∈[﹣6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间.
其中,所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com