
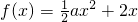 ,g(x)=lnx.
,g(x)=lnx.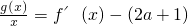 在区间
在区间 内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.
内有且只有两个不相等的实数根?若存在,请求出a的取值范围;若不存在,请说明理由.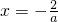 ,
,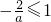 ,解得a≤-2或a>0,所以a>0.
,解得a≤-2或a>0,所以a>0.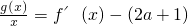 整理为
整理为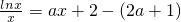 ,
,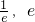 )内有且只有两个不相等的实数根,
)内有且只有两个不相等的实数根,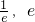 )内有且只有两个零点
)内有且只有两个零点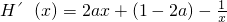 =
=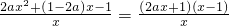
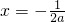 (舍)
(舍)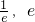 )内有且只有两个不相等的零点,
)内有且只有两个不相等的零点,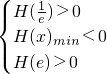
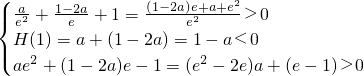
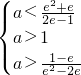
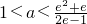 ,
,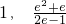 ).
).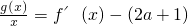 整理为ax2+(1-2a)x-lnx=0构造函数H(x)=ax2+(1-2a)x-lnx(x>0),则原方程在区间
整理为ax2+(1-2a)x-lnx=0构造函数H(x)=ax2+(1-2a)x-lnx(x>0),则原方程在区间 内有且只有两个不相等的实数根即为函数H(x)在区间(
内有且只有两个不相等的实数根即为函数H(x)在区间(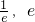 )内有且只有两个零点,根据函数零点存在定理,结合函数的单调性,构造不等式组,解不等式组即可得到结论.
)内有且只有两个零点,根据函数零点存在定理,结合函数的单调性,构造不等式组,解不等式组即可得到结论.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com