
分析 首先,可以设$\frac{y}{x+2}=k$,得到kx-y+2k=0,然后,利用圆心到直线的距离,确定其取值范围;在求解y-2x的取值范围时,可以利用圆的参数方程比较简单.
解答 解:设$\frac{y}{x+2}=k$,
∴y=kx+2k,
∴kx-y+2k=0,
圆心到直线的距离为d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}=1$,
∴-$\frac{\sqrt{3}}{3}$≤k≤$\frac{\sqrt{3}}{3}$,
∴$\frac{y}{x+2}$的取值范围[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$].
再设圆的参数方程为:
$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$,
∴y-2x=sinθ-2cosθ
=$\sqrt{5}$sin(θ-φ),
∴y-2x的取值范围[-$\sqrt{5}$,$\sqrt{5}$].
点评 本题重点考查了圆的参数方程、直线与圆的位置关系等知识,属于中档题.


科目:高中数学 来源:2016-2017学年河北涞水波峰中学高一9月月考数学试卷(解析版) 题型:选择题
以下六个写法中:①{0}∈{0,1,2}; ②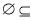 {1,2}; ③
{1,2}; ③ ④{0,1,2}={2,0,1}; ⑤
④{0,1,2}={2,0,1}; ⑤ ; ⑥
; ⑥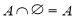 ,正确的个数有( )
,正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com