

| A. | 115种 | B. | 125种 | C. | 135种 | D. | 145种 |
分析 根据题意,分3种情况讨论:1、通过4桥将5个岛屿连成1线,2、任选3岛构成2段折线,再在两端任选1端与另两岛分别连接,3、4桥从同1岛动身与其余4岛连接,分别求出每种情况下的修桥方案数目,由分类计数原理计算可得答案.
解答 解:根据题意,分3种情况讨论:
1、通过4桥将5个岛屿连成1线,有$\frac{1}{2}$×A55=60种方案;
2、任选3岛构成2段折线,再在两端任选1端与另两岛分别连接,有C53×C31×2=60种方案;
3、4桥从同1岛动身与其余4岛连接,有5种方案;
共有60+60+5=125种;
故选:B.
点评 本题考查分类计数原理的运用,关键是分析题意,找全可能的情况.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:选择题
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-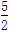 )等于( )
)等于( )
A.-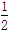 B.-
B.-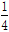 C.
C. 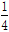 D.
D. 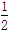
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com