
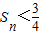 .
.
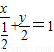 ,直线OC1的方程:y=2x,由此可解得C2的横坐标为
,直线OC1的方程:y=2x,由此可解得C2的横坐标为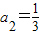 .
.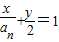 ,联立OC1:y=2x,可解得
,联立OC1:y=2x,可解得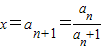 ,由引可知
,由引可知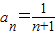 .
.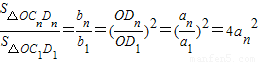 ,由此可知Sn=b1+b2+b3+bn=
,由此可知Sn=b1+b2+b3+bn=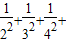
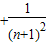 <
<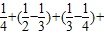
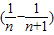 =
=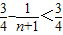 .
. ,1),D1(
,1),D1( ,0),
,0),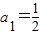 ,
,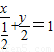 ,直线OC1的方程:y=2x,
,直线OC1的方程:y=2x,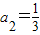 (2分)
(2分)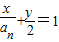 ,联立OC1:y=2x,
,联立OC1:y=2x,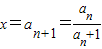 ,∴
,∴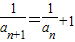 (5分)
(5分)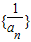 是首项为2公差为1的等差数列,∴
是首项为2公差为1的等差数列,∴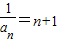 ,∴
,∴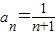 (8分)
(8分)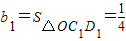 ∵△OCnDn~△OC1D1
∵△OCnDn~△OC1D1 ,
,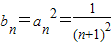 (11分)
(11分)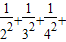
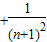
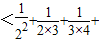 +
+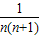
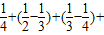
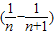
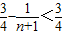 (14分)
(14分)

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
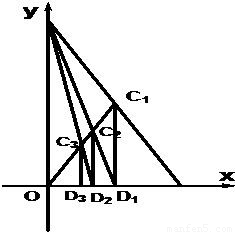
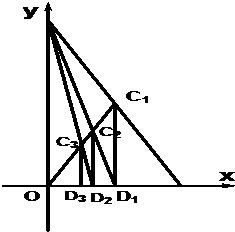 如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).
如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).| 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且| AE |
| EC |
| 2 |
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012江苏高考数学填空题提升练习(14) 题型:022
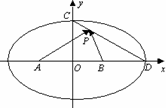
如图,已知A(-1,0)、B(1,0)是椭圆![]() 的长轴上两定点,C,D分别为椭圆的短轴和长轴的端点,P是线段CD上的动点,若
的长轴上两定点,C,D分别为椭圆的短轴和长轴的端点,P是线段CD上的动点,若![]() 的最大值与最小值分别为3、
的最大值与最小值分别为3、![]() ,则椭圆方程为________.
,则椭圆方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
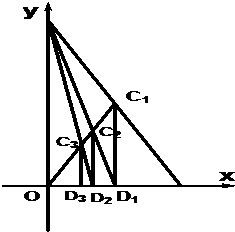 如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).
如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0). .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com