Question

已知a、b、c分别是△ABC的三个内角A、B、C的对边，向量m=(cos，sin)，n=(cos，-sin)，p=(1，sinA)，且u=2(1-m·n)(1+m·n)+p²．

(1)u可以表示为角A的函数u(A)，试求u(A)的表达式；

(2)(文)求函数u(A)的值域；

(理)若角A使u(A)取到最大值，且a=2bcosB，判断此时△ABC的形状．

Answer 1

答案：(1)u=2[1-(m·n)²]+p²

=2[1-(coscos-sinsin)²]+(1+sin²A)

=2(1-cos²)+1+sin²A

=2(1-sin²)+1+sin²A

=2cos²+sin²A+1.

(2)(文)u=1+cosA+2-cos²A=-(cosA)²+.

令cosA=t，则u=-(t)²+．

∵0＜a＜π．∴-1＜cosA＜1-1＜t＜1．

由图知，u(-1)＜u＜u()，即u∈(1，)．

(理)u=1+cosA+2-cos²A=-(cosA)²+．

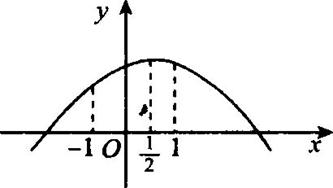
第17题图

∴当cosA=时，

即A=60°时，u取得最大值

由a=2bcosB

可得sinA=2sinBcosB，

即sin2B=sinA=．

∵0＜2B＜，

∴2B=或B=或或.

故△ABC是直角三角形或等边三角形．