Question

设等差数列{a_n}的前n项和为S_n，且S₄=48，a₂+a₅=20．
（1）求数列{a_n}的通项公式；
（2）设b_n=（17-a_n）•2^n-1，求数列{b_n}的前n项和T_n．

Answer 1

解：（1）依题意得
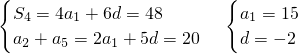
∴a_n=15+（n-1）（-2）=17-2n，
（2）b_n=（17-a_n）•2^n-1=n•2ⁿ
T_n=1•2¹+2•2²+3•2³+…+n•2ⁿ
2T_n=1•2²+2•2³+3•2⁴+…+n•2ⁿ⁺¹两式相减得：
-T_n=2¹+2²+…+2ⁿ-n•2ⁿ⁺¹=
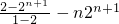
∴T_n=2+（n-1）•2ⁿ⁺¹
分析：（1）根据题意建立关于该等差数列的首项与公差的方程组，从而可求其通项公式；
（2）得到b_n=n•2ⁿ，其前n项和T_n可用错位相减的方法求得．
点评：本题考查数列求和，重点考查学生方程组法求通项，错位相减法求和，注意运算的准确性属于中档题．