
已知某工厂生产 件产品的成本为
件产品的成本为 (元),
(元),
问:(1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
(1) 1000 ;(2) 6000.
【解析】
试题分析:(1)先根据题意设生产x件产品的平均成本为y元,再结合平均成本的含义得出函数y的表达式,最后利用导数求出此函数的最小值即可;
(2)先写出利润函数的解析式,再利用导数求出此函数的极值,从而得出函数的最大值,即可解决问题:要使利润最大,应生产多少件产品..
试题解析:【解析】
(1)设平均成本为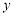 元,则
元,则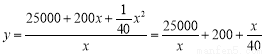 ,
,
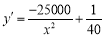 ,令
,令 得
得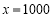 .
.
当在 附近左侧时
附近左侧时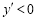 ;
;
在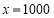 附近右侧时
附近右侧时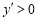 ,故当
,故当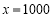 时,
时,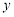 取极小值,而函数只有一个点使
取极小值,而函数只有一个点使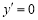 ,故函数在该点处取得最小值,因此,要使平均成本最低,应生产1000件产品. 6分;
,故函数在该点处取得最小值,因此,要使平均成本最低,应生产1000件产品. 6分;
(2)利润函数为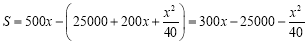 ,
,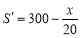 ,
,
令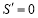 ,得
,得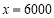 ,当在
,当在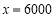 附近左侧时
附近左侧时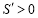 ;在
;在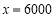 附近右侧时
附近右侧时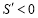 ,故当
,故当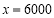 时,
时,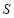 取极大值,而函数只有一个点使
取极大值,而函数只有一个点使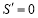 ,故函数在该点处取得最大值,因此,要使利润最大,应生产6000件产品. 12分;
,故函数在该点处取得最大值,因此,要使利润最大,应生产6000件产品. 12分;
考点:导数的应用.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源:2015届内蒙古高二下学期期中考试文科数学试卷(解析版) 题型:选择题
过点且平行于极轴的直线的极坐标方程是( )
A.ρcosθ=4 B.ρsinθ=4 C.ρsinθ= D.ρcosθ=
D.ρcosθ=
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ文科数学试卷(解析版) 题型:填空题
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,则小正方形的边长为 时,盒子容积最大?。

查看答案和解析>>
科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ文科数学试卷(解析版) 题型:选择题
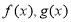 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当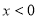 时
时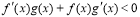 且
且 的解集为( )
的解集为( )
A.(-2,0)∪(2,+∞)
B.(-2,0)∪(0,2)
C.(-∞,-2)∪(2,+∞)
D.(-∞,-2)∪(0,2)
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古高二下学期期末考试理科数学试卷(解析版) 题型:解答题
某研究机构对高三学生的记忆力x和判断力y进行统计分析,所得数据如表所示:
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
画出上表数据的散点图为:

(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =
= x+
x+ .
.
(2)试根据(1)求出的线性回归方程,预测记忆力为9的学生的判断力
( 其中 ,
,  )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com