
【题目】已知函数 ,若方程
,若方程![]() 有两个不等实根
有两个不等实根![]() 、
、![]() ,且
,且![]() ,则实数
,则实数![]() 的取值范围为________
的取值范围为________
【答案】![]()
【解析】
作出函数f(x)的图象,根据分段函数的关系,结合一元二次函数的对称性,利用数形结合进行求解即可.
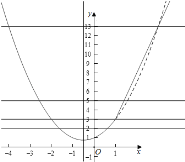
解:作出函数f(x)的图象如图:
由x2+x+1=5x﹣2得x2﹣4x+3=0得x=1或x=3,
即y=x2+x+1与y=5x﹣2的交点坐标为(1,3),(3,12),
当x≤1时,y=x2+x+1=(x![]() )2
)2![]() ,抛物线的对称轴为x
,抛物线的对称轴为x![]() ,
,
若方程f(x)=m有两个不相等的实数根x1、x2,
则m![]() ,
,
若x1+x2<﹣1,
则![]() ,
,
即两个函数的交点(x1、f(x1)),(x2、f(x2))的中点在x![]() 的左侧,
的左侧,
即当x>1时,x2+x+1<5x﹣2,即1<x<3,
此时3<f(x)<13,
即3<m<13,
故答案为:(3,13)


科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数,则下列结论中错误的个数是( )
的导函数,则下列结论中错误的个数是( )
①函数![]() 的值域与
的值域与![]() 的值域相同;
的值域相同;
②若![]() 是函数
是函数![]() 的极值点,则
的极值点,则![]() 是函数
是函数![]() 的零点;
的零点;
③把函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,就可以得到
个单位长度,就可以得到![]() 的图像;
的图像;
④函数![]() 和
和![]() 在区间
在区间![]() 内都是增函数.
内都是增函数.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某沿海地区计划铺设一条电缆联通A,B两地,A地位于东西方向的直线MN上的陆地处,B地位于海上一个灯塔处,在A地用测角器测得![]() ,在A地正西方向4km的点C处,用测角器测得
,在A地正西方向4km的点C处,用测角器测得![]() .拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设
.拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设![]() ,
,![]() ,铺设电缆的总费用为
,铺设电缆的总费用为![]() 万元.
万元.
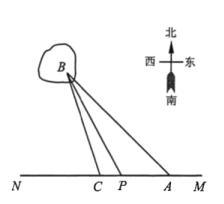
(1)求函数![]() 的解析式;
的解析式;
(2)试问点P选在何处时,铺设的总费用最少,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,半径为
,半径为![]() .
.
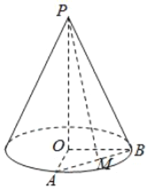
(1)设圆锥的母线长为![]() ,求圆锥的体积;
,求圆锥的体积;
(2)设![]() ,
,![]() 、
、![]() 是底面半径,且
是底面半径,且![]() ,
,![]() 为线段
为线段![]() 的中点,如图.求异面直线
的中点,如图.求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数具有性质
,则称函数具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并证明:①
,并证明:①![]() (
(![]() );②
);②![]() ;
;
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() (
(![]() ,
,![]() ),
),
①求证:对任意![]() ,有
,有![]() ;
;
②是否对任意![]() ,均有
,均有![]() ?若有,给出证明,若没有,给出反例.
?若有,给出证明,若没有,给出反例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com