练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】埃及金字塔是古埃及的帝王（法老）陵墓，世界七大奇迹之一，其中较为著名的是胡夫金字塔．令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿，还有发生在胡夫金字塔上的数字“巧合”．如胡夫金字塔的底部周长如果除以其高度的两倍，得到的商为3.14159，这就是圆周率较为精确的近似值．金字塔底部形为正方形，整个塔形为正四棱锥，经古代能工巧匠建设完成后，底座边长大约230米．因年久风化，顶端剥落10米，则胡夫金字塔现高大约为（ ）

    A.128.5米B.132.5米C.136.5米D.110.5米

    【答案】C

    【解析】

    设出胡夫金字塔原高，根据题意列出等式，解出等式即可根据题意选出答案。

    胡夫金字塔原高为 ，则 ，即米，

    则胡夫金字塔现高大约为136.4米．故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的参数方程为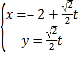：，为参数点的极坐标为，曲线C的极坐标方程为．

    Ⅰ试将曲线C的极坐标方程化为直角坐标方程，并求曲线C的焦点在直角坐标系下的坐标；

    Ⅱ设直线l与曲线C相交于两点A，B，点M为AB的中点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市旅游局为了进一步开发旅游资源，需要了解游客的情况，以便制定相应的策略，在某月中随机抽取甲、乙两个景点各10天的游客数，画出茎叶图如下：若景点甲中的数据的中位数是126，景点乙中的数据的平均数是124.

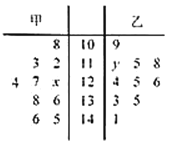
    （1）求，的值；

    （2）若将图中景点甲中的数据作为该景点较长一段时期内的样本数据（视样本频率为概率）.今从这段时期内任取4天，记其中游客数不低于125人的天数为，求概率；

    （3）现从上图的共20天的数据中任取2天的数据（甲、乙两景点中各取1天），记其中游客数不低于115且不高于135人的天数为，求的分布列和期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AB//CD，且.

    （1）证明：平面PAB⊥平面PAD；

    （2）若PA=PD=AB=DC， ，求二面角A-PB-C的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，为矩形，是以为直角的等腰直角三角形，平面平面．

    （Ⅰ）证明：平面平面；

    （Ⅱ）为直线的中点，且，求二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，点M，N分别为线段，的中点，，，．

    （1）证明：；

    （2）求平面与平面所成锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两点，，线段为的直径

    （1）求的方程；

    （2）若经过点的直线被截得的弦长为8，求此直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，从参加环保知识竞赛的学生中抽出名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：

    （1）这一组的频数、频率分别是多少？

    （2）估计这次环保知识竞赛成绩的平均数、众数、中位数。（不要求写过程）

    (3) 从成绩是80分以上（包括80分）的学生中选两人，求他们在同一分数段的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以表示值域为的函数组成的集合，表示具有如下性质的函数组成的集合：对于函数，存在一个正数，使得函数的值域包含于区间。例如，当，时，，。则下列命题中正确的是：（ ）

    A.设函数的定义域为，则“”的充要条件是“，，”

    B.函数的充要条件是有最大值和最小值

    C.若函数，的定义域相同，且，，则

    D.若函数有最大值，则

    查看答案和解析>>

    同步练习册答案