
【题目】某花卉企业引进了数百种不同品种的康乃馨,通过试验田培育,得到了这些康乃馨种子在当地环境下的发芽率,并按发芽率分为![]() 组:
组:![]() 、
、![]() 、
、![]() 、
、![]() 加以统计,得到如图所示的频率分布直方图.企业对康乃馨的种子进行分级,将发芽率不低于
加以统计,得到如图所示的频率分布直方图.企业对康乃馨的种子进行分级,将发芽率不低于![]() 的种子定为“
的种子定为“![]() 级”,发芽率低于
级”,发芽率低于![]() 但不低于
但不低于![]() 的种子定为“
的种子定为“![]() 级”,发芽率低于
级”,发芽率低于![]() 的种子定为“
的种子定为“![]() 级”.
级”.
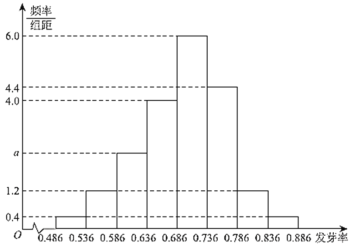
(Ⅰ)现从这些康乃馨种子中随机抽取一种,估计该种子不是“![]() 级”种子的概率;
级”种子的概率;
(Ⅱ)该花卉企业销售花种,且每份“![]() 级”、“
级”、“![]() 级”、“
级”、“![]() 级”康乃馨种子的售价分别为
级”康乃馨种子的售价分别为![]() 元、
元、![]() 元、
元、![]() 元.某人在市场上随机购买了该企业销售的康乃馨种子两份,共花费
元.某人在市场上随机购买了该企业销售的康乃馨种子两份,共花费![]() 元,以频率为概率,求
元,以频率为概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)企业改进了花卉培育技术,使得每种康乃馨种子的发芽率提高到原来的![]() 倍,那么对于这些康乃馨的种子,与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差是否发生变化?若发生变化,是变大了还是变小了?(结论不需要证明).
倍,那么对于这些康乃馨的种子,与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差是否发生变化?若发生变化,是变大了还是变小了?(结论不需要证明).
【答案】(Ⅰ)![]() ;(Ⅱ)分布列详见解析,数学期望为
;(Ⅱ)分布列详见解析,数学期望为![]() ;(Ⅲ)方差变大了.
;(Ⅲ)方差变大了.
【解析】
(Ⅰ)利用频率分布直方图中矩形面积之和为![]() ,求出
,求出![]() 的值,再结合频率分布直方图以及对立事件的概率公式可求得所求事件的概率;
的值,再结合频率分布直方图以及对立事件的概率公式可求得所求事件的概率;
(Ⅱ)由题意可知,随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,计算出随机变量
,计算出随机变量![]() 在不同取值下的概率,由此可列出随机变量
在不同取值下的概率,由此可列出随机变量![]() 的分布列,进而可求得随机变量
的分布列,进而可求得随机变量![]() 的数学期望;
的数学期望;
(Ⅲ)根据离散型随机变量方差的性质可得出结论.
(Ⅰ)设事件![]() 为:“从这些康乃馨种子中随机抽取一种,且该种子不是“
为:“从这些康乃馨种子中随机抽取一种,且该种子不是“![]() 级”种子”,
级”种子”,
由图表,得![]() ,解得
,解得![]() ,
,
由图表,知“![]() 级”种子的频率为
级”种子的频率为![]() ,
,
故可估计从这些康乃馨种子中随机抽取一种,该种子是“![]() 级”的概率为
级”的概率为![]() .
.
因为事件![]() 与事件“从这些康乃馨种子中随机抽取一种,且该种子是“
与事件“从这些康乃馨种子中随机抽取一种,且该种子是“![]() 级”种子”为对立事件,
级”种子”为对立事件,
所以事件![]() 的概率
的概率![]() ;
;
(Ⅱ)由题意,任取一颗种子,恰好是“![]() 级”康乃馨的概率为
级”康乃馨的概率为![]() ,
,
恰好是“![]() 级”康乃馨的概率为
级”康乃馨的概率为![]() ,
,
恰好是“![]() 级”的概率为
级”的概率为![]() .
.
随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
且![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
故![]() 的数学期望
的数学期望![]() .
.
(Ⅲ)与旧的发芽率数据的方差相比,技术改进后发芽率数据的方差变大了.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为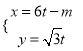 (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 上的动点
上的动点![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
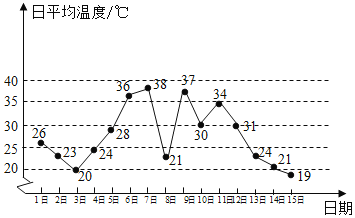
A. 这15天日平均温度的极差为![]()
B. 连续三天日平均温度的方差最大的是7日,8日,9日三天
C. 由折线图能预测16日温度要低于![]()
D. 由折线图能预测本月温度小于![]() 的天数少于温度大于
的天数少于温度大于![]() 的天数
的天数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.

给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
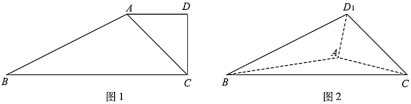
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,点
两点,点![]() 满足
满足![]() .
.
(1)当![]() 的倾斜角为
的倾斜角为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学使用某品牌暖水瓶,其内胆规格如图所示.若水瓶内胆壁厚不计,且内胆如图分为①②③④四个部分,它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱体.若其中圆台部分的体积为![]() ,且水瓶灌满水后盖上瓶塞时水溢出
,且水瓶灌满水后盖上瓶塞时水溢出![]() .记盖上瓶塞后,水瓶的最大盛水量为
.记盖上瓶塞后,水瓶的最大盛水量为![]() ,
,
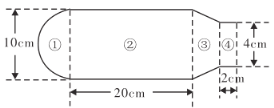
(1)求![]() ;
;
(2)该同学发现:该品牌暖水瓶盛不同体积的热水时,保温效果不同.为了研究保温效果最好时暖水瓶的盛水体积,做以下实验:把盛有最大盛水量![]() 的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温
的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温![]() (单位:℃)与时刻
(单位:℃)与时刻![]() 满足线性回归方程
满足线性回归方程![]() ,通过计算得到下表:
,通过计算得到下表:
倒出体积 | 0 | 30 | 60 | 90 | 120 |
拟合结果 |
|
|
|
|
|
倒出体积 | 150 | 180 | 210 | … | 450 |
拟合结果 |
|
|
| … |
|
注:表中倒出体积![]() (单位:
(单位:![]() )是指从最大盛水量中倒出的那部分水的体积.其中:
)是指从最大盛水量中倒出的那部分水的体积.其中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
令![]() .对于数据
.对于数据![]() ,可求得回归直线为
,可求得回归直线为![]() ,对于数据
,对于数据![]() ,可求得回归直线为
,可求得回归直线为![]() .
.
(ⅰ)指出![]() 的实际意义,并求出回归直线
的实际意义,并求出回归直线![]() 的方程(参考数据:
的方程(参考数据:![]() );
);
(ⅱ)若![]() 与
与![]() 的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且
的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且![]() 取3.14)保温效果最佳?
取3.14)保温效果最佳?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为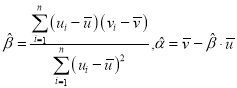 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com