
隔河看两目标A与B,但不能到达,在岸边先选取相距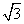 千米的C,D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
千米的C,D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
科目:高中数学 来源: 题型:
已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,-π<φ≤π.若f(x)的最小正周期为6π,且当x=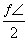 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
A.f(x)在区间[-2π,0]上是增函数
B.f(x)在区间[-3π,-π]上是增函数
C.f(x)在区间[3π,5π]上是减函数
D.f(x)在区间[4π,6π]上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)①证明两角和的余弦公式
C(α+β):cos(α+β)=cos αcos β-sin αsin β;
②由C(α+β)推导两角和的正弦公式
S(α+β):sin(α+β)=sin αcos β+cos αsin β.
(2)已知cos α=-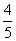 ,
,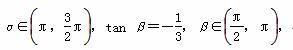 ,
,
求cos(α+β).
查看答案和解析>>
科目:高中数学 来源: 题型:
在某次测量中,在A处测得同一平面方向的B点的仰角是50°,且到A的距离为2,C点的俯角为70°,且到A的距离为3,则B、C间的距离为( )
A. B.
B.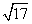
C.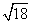 D.
D.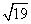
查看答案和解析>>
科目:高中数学 来源: 题型:
一船以每小时15 km的速度向东航行,船在A处看到一个灯塔M在北偏东60°方向,行驶4 h后,船到B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为________ km.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①向量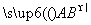 的长度与向量
的长度与向量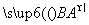 的长度相等;
的长度相等;
②向量a与b平行,则a与b的方向相同或相反;
③两个有共同起点而且相等的向量,其终点必相同;
④两个有公共终点的向量,一定是共线向量;
⑤向量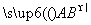 与向量
与向量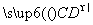 是共线向量,则点A、B、C、D必在同一条直线上.
是共线向量,则点A、B、C、D必在同一条直线上.
其中不正确的个数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于数列{an},“an+1>|an|(n=1,2,…)”是“{an}为递增数列”的( ).
A.必要不充分条件 B.充分不必要条件
C.必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com