


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:走向清华北大同步导读·高二数学(上) 题型:013
设a是三个互异正数a、b、c中的最大数,且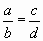 ,则a+d与b+c的大小关系是
,则a+d与b+c的大小关系是
[ ]
A.a+d<b+c B.a+d>b+c
C.a+d=b+c D.无法确定
查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高一数学 人教社(新课标B 2004年初审通过) 人教实验版 题型:013
设平面上有三个互异的点A、B、C,已知![]() ,则△ABC的形状是
,则△ABC的形状是
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等边三角形
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省杭州市建德市新安江中学高一(上)期中数学试卷(解析版) 题型:选择题
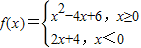 ,若存在互异的三个实数x1,x2,x3,使f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
,若存在互异的三个实数x1,x2,x3,使f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com